Friedrich Schiller Universität Jena
Physikalisch-Astronomisch-Technikwissenschaftliche Fakultät
angefertigt in der Carl Zeiss Jena GmbH
eingereicht von Ralf Arnold
geb. am 06.03.1966
Betriebliche Fachbetreuer: Dr. J. Müller, Dipl.-Ing. M. Chour
Betreuender Hochschullehrer: Prof. Dr. rer. nat. habil. C. Hofmann
Jena, im November 1993
Eine der wichtigsten Forderungen der modernen industriellen Fertigung ist die rationelle und genaue Messung geometrischer Größen /1/. Ein entsprechendes Meßmittel sind Laserinterferometerwegmeßsysteme oder - kurz - Laserwegmeßsysteme, die gegenüber anderen Meßmitteln eine Reihe von Vorzügen besitzen. Die Messungen erfolgen berührungslos, verschleißfrei und innerhalb der durch die Divergenz des Laserstrahls bedingten Grenzen nicht entfernungsgebunden. Der Laserstrahl selbst (Lichtpunkt auf Gegenständen) ist als Justierhilfe nutzbar und kann nie zerstört oder deformiert werden.
Mit modernen, leistungsfähigen Personalcomputern zur Meßwertgewinnung und Auswertung gekoppelt, finden solche Systeme immer breitere Anwendung. Ihre durch die Anwendung der Wellenlänge des Lichtes als Maßstab in Verbindung mit der hohen Kohärenzlänge schmalbandiger Laserlichtquellen hohe Genauigkeit erlaubt den Einsatz von Laserinterferometern zur Kalibrierung mechanischer Meßmittel und Meßmaschinen /2/ einschließlich der Kalibrierung von Fertigungsmaschinen /3/, /4/. Die hohe Kompaktheit moderner Geräte gestattet darüber hinaus ihre Nutzung als direkte Einbaumeßsysteme in Fertigungsmaschinen /5/. Diese Einsatzmöglichkeiten entsprechen dem Trend in der aktuellen Entwicklung nach Erweiterung des Einsatzes der Laserwegmeßsysteme in Werkhallen und -räumen unter nicht exakt definierten Umgebungsbedingungen oder unter nicht exakter Justage.
Um die Einhaltung der durch den Hersteller angegebenen Meßunsicherheit des Laserwegmeßsystems zu garantieren, sind theoretische und experimentelle Untersuchungen der physikalischen und technischen Grenzen bei der Messung geometrischer Größen erforderlich. Der Schwerpunkt dieser Arbeit liegt dabei besonders auf der Untersuchung der möglichen Meßfehler bei Verwendung des Zweifrequenzlaserwegmeßsystems ZLM 300 der Carl Zeiss Jena GmbH als "Optisches Richtlineal" zur Durchführung der Geradheitsmessung. Insbesondere sollen hierbei die Einflüsse der Gravitation und der Atmosphäre (Temperatur und -gradient, Druck und -gradient, Feuchte) sowie ihre mögliche Abhängigkeit von der Meßlänge Beachtung finden. Weiterhin soll der Einfluß des heterodynen Meßprinzips auf die Ergebnisse der Geradheitsmessung untersucht werden.
In der Metrologie verwandte Laserinterferometer werden im wesentlichen in zwei Gruppen unterteilt. Die erste Gruppe bilden die Laserentfernungsmeßsysteme, die die Entfernung absolut zu einem systemintern definierten Nullpunkt messen. Die zweite, am weitesten verbreitete Gruppe bilden die Laserwegmeßsysteme, deren Funktion im wesentlichen auf der Abzählung von Interferenzstreifen bzw. exakt definierten Bruchteilen von Interferenzstreifen beruht. Hierbei ist der Nullpunkt der Abzählung willkürlich wählbar, es handelt sich um ein relativ messendes System. Die Laserwegmeßsysteme werden wiederum unterteilt nach der Polarisationsrichtung des verwandten Lichtes und der Anzahl der genutzten Lichtfrequenzen /6/. Danach unterscheidet man zwischen einmodigen bzw. zweimodigen und parallel bzw. orthogonal zueinander polarisierten Systemen. Hierbei sind Moden transversale, elektromagnetische Schwingungen, die hinsichtlich ihrer Anzahl der Anzahl der Nullstellen orthogonal zur Ausbreitungsrichtung (TEMm,n) und ihrer Frequenz unterschieden werden /7/.
Das zur Realisierung dieser Arbeit zu untersuchende Laserwegmeßsystem ZLM 300 der Carl Zeiss Jena GmbH gehört zur Gruppe der zweimodigen oder auch heterodynen Systeme, wobei die beiden Moden orthogonal zueinander polarisierte TEM0,0-Moden eines HeNe-Lasers der Wellenlänge l = 632,8 nm mit einer Frequenzdifferenz von 640 MHz sind. Das Funktionsprinzip soll im Kapitel 2 beschrieben werden. Zuvor wollen wir uns jedoch kurz mit der Struktur und Ausbreitung der Laserstrahlen beschäftigen.
Laserbündel des TEM0,0-Modus sind (exklusive der Polarisation) in ihrer Verteilung des elektrischen Feldes
| (1.3.1) |
zylindersymmetrisch (Bild 1.3.1.) /7/.
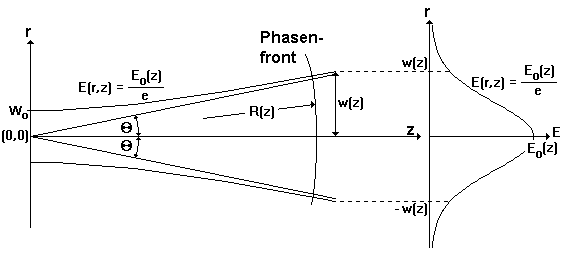
Bild 1.3.1: Achsialer Schnitt und radiale Feldverteilung eines Gauß-Bündels
In Gl.(1.3.1) bedeuten z die Koordinate in Ausbreitungsrichtung (identische der Zylinderachse), r den Abstand senkrecht dazu und w den Radius der Feldverteilung bezogen auf den Abfall der Feldstärke auf 1/e des Maximalwertes E0. Aus (1.3.1) folgt die Intensitätsverteilung
| (1.3.2) |
wobei aus Energieerhaltungsgründen
| (1.3.3) |
gilt.
Der Durchmesser des Bündels 2w wird durch den Abfall beiderseits der Symmetrieachse auf 1/e2 der Intensität definiert. In diesem Durchmesser sind 86% der Laserleistung enthalten, wie man durch Ausführung des Leistungsintegrals ermitteln kann. Der kleinste auftretende Durchmesser des Bündels wird als Taille bezeichnet. Alle Eigenschaften Gauß’scher Bündel sind durch Lage z0 und Größe w0 sowie Leistung P0 in der Taille und Wellenlänge l vollständig charakterisiert. Aus ihnen lassen sich die Größen Rayleigh-Länge
| (1.3.4) |
Strahlradius (vgl. Bild 1.3.1)
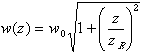 |
(1.3.5) |
und Krümmungsradius (vgl. Bild 1.3.1) der Wellenfronten
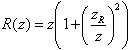 |
(1.3.6) |
ermitteln. Die Rayleigh-Länge ist die Länge, an der sich der Strahlquerschnitt (Fläche) verdoppelt hat. Sie wird als Grenze zwischen Nah- und Fernfeld angesehen, da in ihr die Krümmung der Wellenfronten maximal ist. Die Abhängigkeit des Strahlradius w(z) von der Ausbreitungsrichtung z kann durch eine Hyperbel dargestellt werden, die sich asymptotisch den unter dem Winkel
| (1.3.7) |
zur Symmetrieachse stehenden Geraden annähert. Diese Geraden schneiden die Achse in der Taille. Hervorgehoben sei hier die indirekte Proportionalität von Taillengröße und Divergenzwinkel.
Bildet man Gauß-Bündel mit Hilfe von Linsen ab, ergibt sich eine neue Taille der Lage z0' und Größe w0', die wiederum das Bündel vollständig beschreibt. An dieser Stelle sei auf weiterführende Literatur /7/, /8/ verwiesen.
Aus von Teichmann und Ziesemann in der Carl Zeiss Jena GmbH gewonnenen Meßwerten des Profils des den Laserblock des ZLM 300 (vgl. Kap. 2) verlassenden Strahlenbündels wurden unter Interpolation der 1/e2-Werte die Bündeldurchmesser (Tabelle 1.3.2) ermittelt. Daraus läßt sich die Größe und Lage der Strahltaille abschätzen.
Tabelle 1.3.2: Durchmesser 2w in mm der Bündel verschiedener Laserblöcke des ZLM 300
Entfernung vom Laserblock
Laserbl. Nr.
12 m
16 m
18 m
20 m
22 m
24 m
1
6,10
5,15
6,35
6,40
6,45
2
5,75
5,65
5,70
5,95
5,95
3
6,05
5,95
6,05
6,10
6,20
4
5,70
5,55
5,40
5,45
5,60
Die Taille besitzt einen Durchmesser
| (1.3.8) |
und eine Entfernung vom Austritt des Laserstrahls aus dem Laserblock
| (1.3.9) |
Nach (1.3.7) besitzt das Bündel eine Divergenz
| (1.3.10) |
Die Aufweitung des Durchmessers im Ergebnis der Divergenz des Bündels beträgt für z < 10 m
| (1.3.11) |
und liegt damit im Bereich des Meßfehlers der Taillendurchmessers. Daher können wir unser Gauß-Bündel in guter Näherung als Parallelbündel betrachten. Die Bezeichnung "Strahl" soll daher im folgenden (sofern nicht explizit anders erwähnt) für das Bündel stehen, wobei die Lage des Strahles mit der Symmetrieachse des Gauß-Bündels identisch sein soll.
Der dem Stand der Technik entsprechende Grundaufbau des ZLM 300 (Bild 2.1.1) gehört zum Typ der Michelson-Interferometer und besteht aus einem Laserblock, der Lasersteuerung, der Auswerteelektronik, einem Personalcomputer (im weiteren PC), einem Polarisationsstrahlteiler (P) und zwei Tripel-Prismen (a und b). Das Prisma (b), welches sich im Meßarm (2) des Interferometers befindet, dient hierbei als bewegliches Meßprisma, das Prisma (a) dient als Referenzprisma und befindet sich im Referenzarm (1).
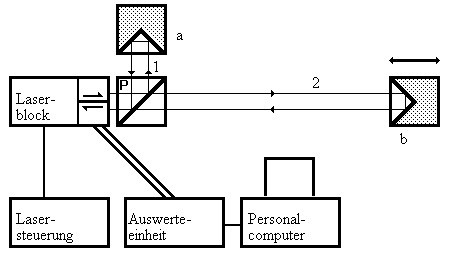
Bild 2.1.1: Grundaufbau eines Laserwegmeßsystems, die Buchstaben bezeichnen das Referenztripel-prisma (a), das Meßtripelprisma (b) und den Polarisationsstrahlteiler (P), die Zahlen bezeichnen den Referenzarm (1) und den Meßarm (2) des Interferometers
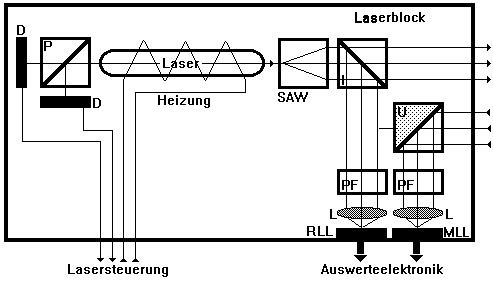
Bild 2.1.2: Aufbau des Laserblocks, die Buchstaben bezeichnen Detektoren (D), Polariations- (P) und Intensitätsstrahlteiler (I), Polarisationsfilter (PF), Linsen (L), das Umlenkprisma (U), die Strahlaufweitung (SAW) und den Meß- und Referenzlichtwellenleiter (MLL, RLL)
Laserblock mit Lasersteuerung: Der Laserblock (Bild 2.1.2) enthält einen HeNe-Gaslaser, der nach dem Jenoptik-Firmenprospekt /9/ einen Strahl mit folgenden Parametern erzeugt:
Die angegebene zulässige optische Rückkopplung von kleiner als 10-5 erscheint unrealistisch, da sie mit vertretbarem ökonomischen Aufwand nicht erfüllbar ist. Dies entspricht der Forderung nach einer Reflektivität R<0,001% der optischen Bauteile. Nach eigenen Messungen arbeitet der Laser bis zu einer maximalen Rückkopplung in den Laserblock von 0,05% störungsfrei.
Der Laser besteht aus einer als Innenspiegelresonator ausgebildeten Glasküvette, die alle HeNe-lasertypischen Baugruppen beinhaltet.
Die Anordnung links des Lasers im Bild 2.1.2 dient der Frequenzstabilisierung /10/. Dazu spaltet der Polarisationsteiler (P) den Strahl in seine beiden, orthogonal polarisierten Komponenten auf, deren Intensitäten mittels der beiden Detektoren (D) in elektrische Signale umgewandelt und der Lasersteuerung zugeführt werden. Entsprechend der Differenz dieser Signale erfolgt die Steuerung des Stromflusses durch die außen auf den Innenspiegelresonator aufgedampfte Heizung, so daß die Resonatorlänge konstant bleibt. Die Differenzintensität beider Moden bildet das Regelungskriterium. Im Fall ihres Verschwindens besitzen beide Moden die gleiche Intensität und liegen damit stabil und symmetrisch zum Maximum der Verstärkungskurve des Laserüberganges.
Rechts des Resonators befindet sich die Strahlaufweitungsanordnung (SAW), die den Laserstrahl auf einen mittleren Durchmesser von 6 mm erweitert. Dadurch wird eine höhere Richtungsstabilität und eine geringere Strahldivergenz erreicht. Der aufgeweitete Strahl wird anschließend durch einen (1:1)-Intensitätsstrahlteiler (I) geteilt.
Ein Teil des Lichtes gelangt über einen Polarisationsfilter (PF) und eine Linse (L) in den Referenz-Lichtleiter (RLL), welcher das Licht zur Auswerteeinheit (Bild 2.1.1) führt. Dabei besitzt der Polarisationsfilter (PF) eine azimutale Orientierung von 45&#deg; zwischen den Schwingungsebenen der beiden Lasermoden. Er bringt in seiner Durchlaßebene beide Moden mit gleichen Amplituden zur Interferenz. In der Auswerteeinheit werden diese Interferenzen in elektrische Signale umgewandelt und der Weiterverarbeitung zugeführt.
Das den Intensitätsteiler (Bild 2.1.2) geradlinig passierende Licht verläßt durch eine Öffnung den Laserblock und dient als Eingangsstrahl des Interferometers (Bild 2.1.1) bzw. anderer, noch später zu besprechender Interferometeranordnungen.
Interferometeranordnung:
Das eigentliche Interferometer des Laserwegmeßsystems besteht im einfachsten Fall (Bild 2.1.1) aus einen Polarisationsstrahlteiler (P) und zwei Tripelprismen (a, b). Der Polarisationsstrahlteiler enthält eine dielektrische Schicht, die die beiden orthogonal zueinander polarisierten Lichtwellen voneinander trennt, indem sie eine Welle durchläßt, die andere aber reflektiert. Dazu macht es sich erforderlich, die Orientierung des Polarisationsstrahlteilers so zu wählen, daß die Schwingungsrichtungen der Lasermoden genau orthogonal bzw. parallel zu ihrer Einfallsebene auf der dielektrischen Schicht ausgerichtet sind. Da die aus der Nichterfüllung dieser Forderung resultierenden Meßfehler bereits von Walke /11/ untersucht wurden, soll die Erfüllung der Forderung im weiteren immer als gegeben vorausgesetzt werden. Das in den Referenzarm (1) des Interferometers gelangende Licht der Frequenz n2 < n1 wird am feststehenden Prisma (a) und das in den Meßarm (2) gelangende Licht der Frequenz n1 am längs der Strahlrichtung beweglichen Prisma (b) reflektiert. Dabei erfahren die reflektierten Strahlen einen Parallelversatz gegenüber den einfallenden Strahlen. Dieser Versatz ist unbedingt erforderlich, da er einen Rückfall der reflektierten Strahlen in den Resonator verhindert. Wäre dies nicht gegeben, würden der Auskoppelspiegel des Laserresonators und die beiden Tripelprismen selbst Resonatoren bilden, die einen stabilen Betrieb des Lasers verhinderten. Ebenfalls aus diesem Grund macht sich eine Entspiegelung aller (einschließlich der im Laserblock lokalisierten) Flächen der Anordnung erforderlich.
Bewegt sich das Meßprisma (b) mit der Geschwindigkeit v > 0 vom Strahlteiler (P) weg, so erfährt die reflektierte Welle eine von der Frequenz n1 und der Lichtgeschwindigkeit im Ausbreitungsmedium c abhängige Dopplerverschiebung Dn1
| (2.1.1) |
die zu einer Frequenz n' der reflektierten Welle von
| (2.1.2) |
führt.
Beide von den Tripelspiegeln reflektierten Signale vereinigen sich im Strahlteiler (P) und verlaufen durch eine zweite Öffnung des Laserblocks in denselben zurück.
Im Laserblock (Bild 2.1.2) wird der ankommende Strahl über ein Umlenkprisma (U), einen Polarisations-filter (PF), eine Linse (L) in den Meß-Lichtleiter (MLL) eingekoppelt und von diesem ebenfalls zur Auswerteeinheit geführt. Die Funktion dieser Bauteile ist mit den oben beschriebenen identisch.
Auswerteeinheit und Personalcomputer:
In der Auswerteeinheit /12/ erfolgt die Umwandlung der Lichtsignale in elektrische Signale. Dazu finden Avalache-Fotodioden Verwendung. Diese wandeln die Intensität I des aus den beiden Teilwellen E1,2
| (2.1.3,4) |
der Amplitude E1,2, der Frequenz n1,2 und der Anfangsphase f1,2 resultierenden aus dem Referenzwellenleiter kommenden Referenz-Interferenzsignales
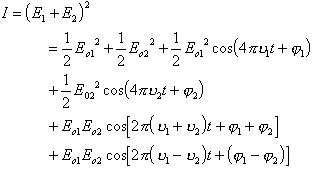 |
(2.1.5) |
in ein proportionales, elektrisches Signal Iel um, wobei die Trägheit der Dioden über alle Frequenzen > 1010 Hz mittelt. Unter Verwendung der Differenzfrequenz nB beider Lasermoden erhält man ein elektrisches Referenz-Signal der Form
| (2.1.6) |
mit C als Summe aller konstanten Anteile. Nach Nullsetzung der Differenz der Anfangsphasen und Filterung der konstanten Anteile folgt
| (2.1.6a) |
Analog ergibt sich das aus dem Licht des Meßlichtwellenleiters erzeugte, elektrische Meßsignal
| (2.1.7) |
Die Signale (2.1.6a) und (2.1.7) werden in einem Stehwellen- (Phasen-) interpolator /12/, /13/ überlagert. Als Resultat erhält man die gesuchte Dopplerfrequenz (2.1.1), die in einem Komperator digitalisiert wird. Ein nachgeschalteter Zähler erfaßt die Anzahl der Nulldurchgänge N unter Berücksichtigung des Vorzeichens der Dopplerfrequenz vom Zeitpunkt t0 des Rücksetzens des Zählers bis zum Zeitpunkt t
| (2.1.8) |
Durch Einsetzen von Gl. (2.1.1) in Gl. (2.1.8) erhält man
|
(2.1.8a) |
unter Nutzung des zurückgelegten Weges seit Rücksetzung der Anzeige zum Zeitpunkt t0
| (2.1.9) | |
| (2.1.10) |
ergibt sich der Zusammenhang zwischen dem zurückgelegten Weg x und den durch den Zähler an die Auswerteeinheit übermittelten Zählwert
| (2.1.8b) |
In der Auswerteeinheit wird die Umkehrung der Gl. (2.1.8b)
| (2.1.8c) |
genutzt, um den Anzeigewert xT des Meßsystems aus den Zählerwerten zu ermitteln. Die angezeigte Wegstrecke xT entspricht damit der zurückgelegten Wegstrecke x, wie durch Einsetzten von Gl. (2.1.8b) in Gl. (2.1.8c) leicht ermittelt werden. Da die Kapazität des Zählers auf 20 MHz beschränkt ist, ergibt sich eine maximal registrierbare Geschwindigkeit von vmax = 6,33 ms-1.
Die Auflösung - gerastetes elektronisches Inkrement (d.h. es handelt sich um echte Triggerpunkte, nicht um Interpolation) - des Stehwelleninterpolators der Auswerteelektronik beträgt konstruktiv bedingt
| (2.1.11) |
Bezieht man dies auf die Anordnung des Bildes 2.1.1, so ergibt sich unter Nutzung von Gl. (2.1.8c) und Gl. (2.1.11) ein Inkrement für Distanzmessungen mit Tripelprismen (kleinster registrierbarer Wegschritt) von
| (2.1.12) |
Die Anordnung nach Bild 2.1.1 stellt natürlich nur den einfachsten Fall eines möglichen Interferometeraufbaus entsprechend des Standes der Technik dar. Zur umfassenden Nutzung eines Laserwegmeßsystems ist es deshalb erforderlich, sich mit weiteren möglichen Anordnungen bekanntzumachen. Da hierbei der Aufbau des Laserblocks, der Lasersteuerung und der Auswerteeinheit einschließlich PC unverändert bleibt, soll auf deren Darstellung im weiteren verzichtet werden.
Eine erste mögliche Meßanordnung wurde bereits im vorhergehenden Kapitel beschrieben. Eine weitere Möglichkeit bietet die Messung unter Verwendung eines Planspiegelinterferometers (Bild 2.2.1).
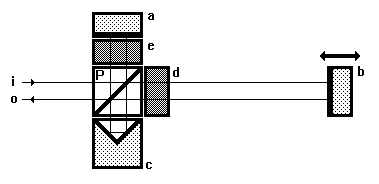
Bild 2.2.1: Planspiegelinterferometer, bestehend aus Planspiegeln (a, b), Polarisationsstrahlteiler (P), Tripelprisma (c), und l/4-Platten (d, e), mit einfallendem (i) und austretendem (o) Strahl
Dazu werden die beiden orthogonal zueinander polarisierten Moden des Inputstrahls (i) im Polarisations-teiler (P) getrennt und zum Meß- (b) beziehungsweise Referenzspiegel (a) geleitet. Dabei passieren beide Teilstrahlen die unter einem Azimut von 45&#deg; zu ihren Polarisationsrichtungen stehenden l/4-Platten (d, e), werden an den Spiegeln reflektiert und passieren erneut die l/4-Platten. Im Ergebnis der doppelten Einwirkung der /4-Platten sind die Polarisationsebenen beider Teilstrahlen um jeweils 90&#deg; gedreht. Das bedeutet, daß der Referenzstrahl nicht wie eingangs am Polarisationsstrahlteiler reflektiert, sondern ihn in Richtung des Tripelprismas (c) passiert. Analog erfolgt eine Reflexion des Meßstrahles an der Polarisationsteilerschicht in Richtung des Tripelprismas (c). Infolge der sich anschließenden Reflexion am Tripelprisma erhalten beide Strahlen den notwendigen Parallelversatz. Sie gelangen über den Polarisationsstrahlteiler in ihre Interferometerarme zurück. Nach erneuter Reflexion an den Spiegeln und doppeltem Passieren der l/4-Platten sind die Polarisationsebenen der beiden Teilstrahlen erneut um 90&#deg; gedreht und damit mit denen des Inputstrahls (i) identisch. Sie werden im Polarisationsstrahlteiler zum Outputstrahl (o) vereinigt. Als weiteres Beispiel ist solch eine konkrete Anordnung in /14/ beschrieben.
Aufgrund der aus der doppelten Reflexion beider Strahlen an den Spiegeln folgenden doppelten optischen Interpolation verändert sich Gl. (2.1.8c) zu
| (2.1.8d) |
woraus sich unter Verwendung der Gl. (2.1.11) das Inkrement für Distanzmessungen mit dem Planspiegelinterferometer
| (2.2.1) |
ergibt.
Eine weitere Variante von Interferometeranordnungen bilden die Differenz-Interferometer (oder auch Interferometer mit Kompensationsstrecke), deren Sinn darin besteht, die Totwege - der Totweg ist die Weglängendifferenz zwischen Meß- und Referenzstrahl - zu minimieren und damit äußere Einflüsse zu kompensieren, da sich diese dann auf Meß- und Referenzstrahl gleichzeitig auswirken. Dazu müssen die Anordnungen entsprechend der Bilder 2.2.2 und 2.2.1 leicht modifiziert werden, es entstehen Anordnungen nach Bild 2.2.2 und 2.2.3. Die Funktionen der einzelnen Elemente entsprechen denen der Bilder 2.1.1 und 2.2.1, daher soll hier auf eine detaillierte Beschreibung verzichtet werden. Ein weiteres Ausführungsbeispiel ist in /15/ angegeben.
Eine andere Gattung der wegmessenden Interferometer bilden die symmetrischen Differenz-Interferometer, meist in der Form der Differenzspiegelinterferometer verwandt. Diese unterscheiden sich von den unsymmetrischen Interferometern dadurch, daß Meß- und Referenzstrahlenwege hinsichtlich der in ihnen angeordneten Bauelemente völlig äquivalent sind. Eine Unsymmetrie, wie sie beispielsweise das Element (f) im Bild 2.2.3 darstellt, wird vermieden. Beispielhaft befindet sich die Beschreibung solch eines Interferometers in /12/ beziehungsweise /16/.
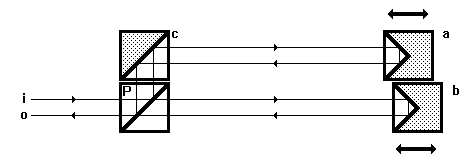
Bild 2.2.2: Differenztripelprismeninterferometer, bestehend aus Tripelprismen (a, b), Polarisationsstrahlteiler (P) und Umlenkprisma (c), mit einfallendem (i) und austretendem (o) Strahl
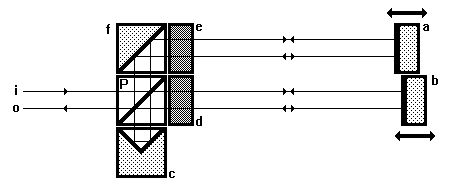
Bild 2.2.3: Differenzplanspiegelinterferometer, bestehend aus Planspiegeln (a, b), Polarisationsstrahlteiler (P), Tripelprisma (c), l/4-Platten (d, e) und Umlenkprisma (f), mit einfallendem (i) und austretendem (o) Strahl
Damit soll die Aufzählung der grundlegenden Interferometertypen abgeschlossen werden. Sie diente zur Erlangung eines Überblickes sowie als Grundlage folgender Ausführungen und erhebt keinen Anspruch auf Vollständigkeit.
Ein weiteres Einsatzgebiet der Laserinterferometrie bildet die Messung von Winkeln, deren Spezifikation der folgende Abschnitt gewidmet werden soll.
Winkelmessende Interferometersyteme werden in der Technik zur Messung von Roll-, Nick- und Gierwinkeln (Bild 2.2.4) verwendet. Die Drehachse des Rollwinkels ist durch den translatorischen Freiheitsgrad des technischen Objektes bestimmt. Die Achsen der Nick- und Gierwinkel liegen orthogonal dazu, wobei die Roll- und die Nickachse gemeinsam die Hauptführungsebene (Bild 2.2.4, schraffiert) bilden.
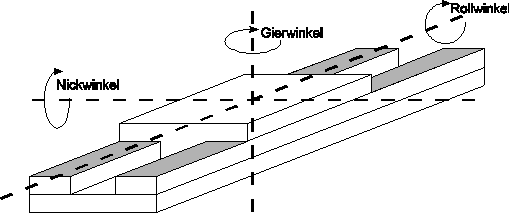
Bild 2.2.4: Definition der Winkel in der Technik
Die Messung der Winkel wird über ausgewählte Dreiecksbeziehungen auf Differenzmessungen von Wegen zurückgeführt. Die Messung von Nick- und Gierwinkeln (Bild 2.2.5, Bild 2.2.6) erfolgt entsprechend der Dreiecksbeziehung für den Kippwinkel a.
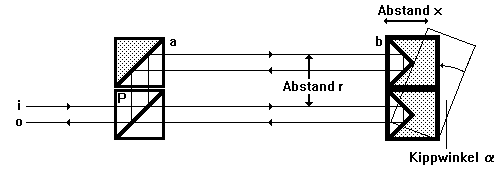
Bild 2.2.5: Anordnung zur Messung von Winkeln, bestehend aus Umlenkprisma (a),Tripelprismen (b) und Polarisationsstrahlteiler (P), mit einfallendem (i) und austretendem (o) Strahl
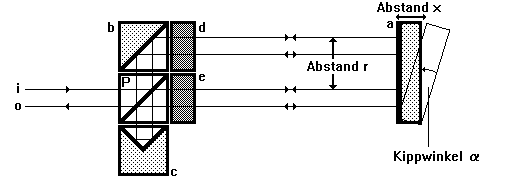
Bild 2.2.6: Anordnung zur Messung von Winkeln, bestehend aus Planspiegel (a), Umlenkprisma (b), Polarisationsstrahlteiler (P), Tripelprisma (c) und l/4-Platten (d, e,) mit einfallendem (i) und austretendem (o) Strahl
Die Abstände r und x der sich in der Ebene senkrecht zur Achse des zu messenden Winkels befindlichen Laserstrahlen bilden mit a den Zusammenhang
| (2.2.2) |
woraus unter Verwendung der Näherung für kleine (Kipp-)Winkel sina = a
| (2.2.3) |
resultiert. Deshalb können nur kleine Winkel gemessen werden. Der Nullpunkt des Winkels im physikalischen Sinne liegt dabei näherungsbedingt in der senkrecht zu den parallelen Meßstrahlen stehenden Ebene. Die Lage des Nullpunktes im Sinne des Anwenders ist durch die Lage bei Rücksetzung des Interferometers (vgl. Kap. 2.1) gegeben. Bei dieser Rücksetzung sollte auf möglichst gute Übereinstimmung mit dem physikalische Nullpunkt geachtet werden.
Ersetzt man nun x in Gl. (2.2.3) mit Hilfe der Gln. (2.1.8c) bzw. (2.1.8d), dann ergeben sich die Meßgleichungen für Winkelmessungen mit Tripelprismen (Anordnung nach Bild 2.2.5)
| (2.2.4) |
beziehungsweise für die Winkelmessung mit Planspiegeln (Anordnung nach Bild 2.2.6)
| (2.2.5) |
woraus wiederum unter Verwendung des elektronischen Inkrements (Gl. (2.1.11)) die Inkremente für die Winkelmessung mit Tripelprismen
| (2.2.6) |
und für die Winkelmessung mit Planspiegeln
| (2.2.7) |
folgen. Unter Nutzung des am ZLM 300 konstruktiv vorgegebenen Abstandes von r = 40 mm ergibt sich das Winkelinkrement für die Messung mit Tripelprismen zu
| (2.2.8) |
bzw. das Winkelinkrement für die Messung mit Planspiegeln zu
| (2.2.9) |
Weitere mögliche Meßanordnungen sind in /17/ und /18/ angegeben.
Etwas schwieriger gestaltet sich die Messung des Rollwinkels, da dessen Drehachse senkrecht zur Ausbreitungsrichtung der Laserstrahlen liegt. Die Behandlung dieses Problems erfolgt ähnlich dem der Geradheitsmessung. Daher ist es ratsam, sich zuerst mit den Anordnungen der Geradheitsmessung vertraut zu machen.
Das Ziel der Geradheitsmessung besteht darin, die zur Bewegungsrichtung senkrechte Abweichung (Geradheitsabweichung) einer als geradlinig geforderten Bewegung von der exakten Gerade zu ermitteln. Als Geradheitsnormal dient die in der Ebene der beiden Normalen der Flächen des Winkelspiegels (b) in Bild 2.2.7 liegende Symmetrieachse des Winkelspiegels. Die Ausbreitungsrichtung der zur Messung verwendeten Laserstrahlung muß dabei mit der Bewegungsrichtung des die Gerade beschreibenden Meßobjektes und mit der Richtung des Geradheitsnormals übereinstimmen. Da diese Übereinstimmung, bedingt durch Justierfehler, nie exakt gewährleistet werden kann, stimmt per Definition die aus den über der Ortskoordinate der Bewegung aufgetragenen Meßwerten errechnete Ausgleichsgerade mit der Normalgerade überein. Gemessen wird die Geradheitsabweichung in der durch die Meß- (M) und Referenzstrahlen (R) gebildeten Ebene (Bild 2.2.7, schraffiert) der zur Messung verwandten Laserstrahlen. Der in Bild 2.2.7 dargestellte Strahlteiler wurde durch Teichmann, Carl Zeiss Jena, konstruiert; die Anordnung Doppelkeil-Winkelspiegel entspricht dem Stand der Technik.
Der beim Betrachten des Bildes 2.2.7 in der vorderen Ebene liegende Inputstrahl (i) wird an der Polarisationsteilerschicht (c) in Meß- (M) und Referenzstrahl (R) aufgespaltet. Beim Passieren der l/2-Platte (e) erfolgt eine Drehung der Polarisationsebene in die des Meßstrahles. Beide Strahlen verlassen durch die l/4-Platte (f) den Teiler (T) mit zirkularer Polarisation. Das Doppelkeilprisma (a) lenkt die Meß- und Referenzstrahlen unter stets gleichen Winkeln ab, der Winkelspiegel reflektiert die stets im Lot einfallenden Strahlen in sich zurück. Bei erneuter Passage der l/4-Platte (f) erlangen beide Strahlen wieder eine lineare Polarisation, deren Ebene um 90&#deg; gegen die des einfallenden Meßstrahles gedreht wurde. Daher werden Meß- und Referenzstrahl an der Polarisationsteilerschicht (c) reflektiert. Sie gelangen in das Dachkantprisma (d), das beide Strahlen unter Parallelversatz zur hinteren Ebene der Bildes 2.2.7 in den Strahlteiler zurückwirft. Anschließend durchlaufen sie die hintere Bildebene in analoger Weise und verlassen, zum Outputstrahl (o) wiedervereinigt, den Teiler (T).
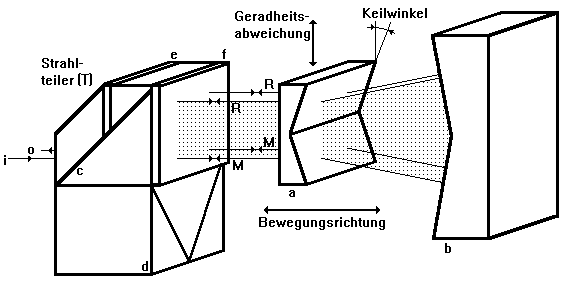
Bild 2.2.7: Anordnung zur Geradheitsmessung, bestehend aus Doppelkeilprisma (a), Winkelspiegel (b), und Strahlteiler (T), der eine Polarisationsteilerschicht (c), ein Dachkantprisma (d), eine l/2-Platte (e) und eine l/4-Platte (f) enthält
Zur Messung der Geradheit der Bewegung eines Objektes muß das Doppelkeilprisma fest mit diesem verbunden sein. Infolge vorhandener Abweichungen von der Geradheit verschiebt sich das Doppelkeilprisma mit dem Keilwinkel k um eine Geradheitsabweichung zg (Strecke BD in Bild 2.2.8) senkrecht zu seiner Bewegungsrichtung und erzeugt dadurch eine optische Weglängendifferenz Dx.
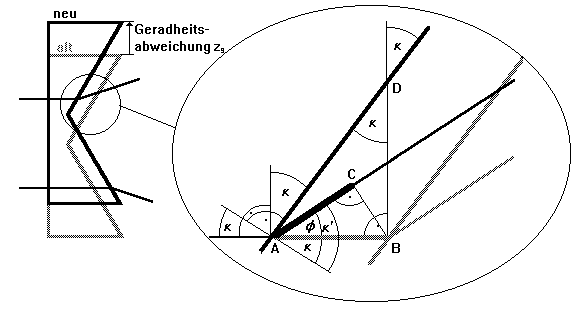
Bild 2.2.8: Skizze zur Ableitung der optischen Wegdifferenz Dx als Funktion des Keilwinkels k und der Geradheitsabweichung zg
Diese berechnet sich pro Referenzstrahl (oberes Strahlenpaar im Bild 2.2.7) zu
| (2.2.10) |
und analog pro Meßstrahl (unteres Strahlenpaar im Bild 2.2.7) zu
| (2.2.10a) |
woraus am Beispiel eines Referenzstrahles (Bild 2.2.8) unter Berücksichtigung der Dreiecksrelationen, der Geradheitsabweichung ![]() , der Relationen
, der Relationen
| (2.2.11) |
und
| (2.2.12) |
und des Brechungsgesetzes
| (2.2.13) |
die Gleichung
| (2.2.14) |
folgt. Nähert man nun Gl. (2.2.11a) mit Hilfe der Relation sin x = x , dann ergibt sich
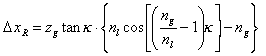 |
(2.2.15) |
In Analogie erhält man
| (2.2.15a) |
Berücksichtigt man das doppelte Vorhandensein von Meß- u. Referenzstrahl (doppelte optische Interpolation) durch den Faktor 2 und berechnet die Differenz von Meß- und Referenzstrahlengang der Anordnung nach Bild 2.2.7
| (2.2.16) |
dann erhält man durch Einsetzen von Gl. (2.2.15) und Gl. (2.2.15a) in Gl. (2.2.16) den linearen Zusammenhang Dx = f(z)
| (2.2.17) |
Betrachtet man die Werte seit der letzten Rücksetzung der Meßanordnung, stellt Gl. (2.2.17) nach z um und setzt Gl. (2.1.8c) ein, dann erhält man den Zusammenhang
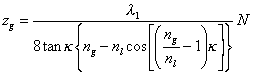 |
(2.2.18) |
Für das ZLM 300 stehen je eine Doppelkeilprisma-Winkelspiegelkombination für eine maximale Meßentfernung von 2m und 10m zur Verfügung. Durch Einsetzen der Daten für
in Gl. (2.2.15) ergeben sich die Werte für den Zusammenhang zwischen Geradheitsabweichung und optischer Weglängendifferenz für
beziehungsweise durch Einsetzen in Gl. (2.2.18) die Meßgleichungen für
Unter Verwendung von Gl. (2.1.11) folgen die Inkremente für
Die Ergebnisse der Geradheitsmessungen werden üblicherweise über der Ortskoordinate der zu vermessenden Gerade angegeben. Diese Ortskoordinate kann bei der Abnahme von Werkzeug- oder Koordinatenmeßmaschinen aus der Maschinensteuerung entnommen werden, in anderen Fällen muß eine separate Messung erfolgen. Dabei ist zur Vermeidung von Meßfehlern bei dynamischen Messungen die exakte Gleichheit der Meßzeitpunkte der Orts- und Geradheitsmeßwerte zu gewährleisten.
Weitere mögliche Anordnungen zur Geradheitsmessung sind in /19/ und /20/ beschrieben, auf eine nähere Spezifizierung dieser Anordnungen soll verzichtet werden.
Die Messung der Ebenheit wird auf einzelne Geradheitsmessungen zurückgeführt. Sie erfolgen entlang ausgewählter Geraden der Ebene. Gebräuchlich sind Messungen nach dem "Union Jack"- oder dem "Cross Jack"-Muster /21/, das heißt, man vermißt die im Muster enthaltenen Strecken einzeln auf Geradheit. Die Werte der einzelnen Geradheitsmessungen werden numerisch durch Interpolation und Extrapolation so aufeinander angepaßt /21/, daß alle Schnittpunkte der Meßlinien jeweils gleiche Geradheitsabweichungen besitzen. Die Ortskoordinaten der einzelnen Meßpunkte in der Ebene müssen simultan, separat gemessen werden, es gelten die weiter oben zur Geradheitsmessung getroffenen Aussagen.
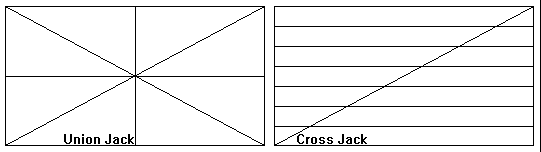
Bild 2.2.9: Möglichkeiten der Zurückführung der Ebenheitsmessung auf einzelne Geradheitsmessungen
Nach erfolgten Aussagen zur Geradheitsmessung soll nun auf die Rollwinkelmessung eingegangen werden. Sie erfolgt in zur Geradheitsmessung ähnlicher Weise, das heißt, sie kann auf zwei simultane, separate Geradheitsmeßanordnungen nach Bild 2.2.7 zurückgeführt werden, wobei die verwendeten Bauteile aus jeweils einem größeren Bauteil bestehen (Bild 2.2.10).
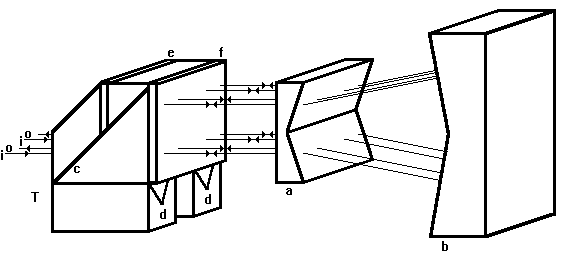
Bild 2.2.10: Anordnung zur Rollwinkelmessung, bestehend aus Doppelkeilprisma (a), Winkelspiegel (b), Strahlteiler (T) mit Polarisationsteilerschicht (c), Dachkantprismen (d), l/2-Platte (e) und l/4-Platte (f) und einfallenden (i) und austretenden (o) Strahlen
Wenn das Doppelkeilprisma (a) im Rollwinkel verändert wird, entstehen am vorderen bzw. hinteren Strahlengang Geradheitsabweichungen, aus denen die Veränderung des Rollwinkels und die Lage der Drehachse bezüglich der im Bild 2.2.10 in die Tiefe gerichteten Koordinate ermittelt werden kann. Anstelle einer Bewegung des Doppelkeilprismas (a) kann man dieses auch in Ruhe belassen und den Winkelspiegel (b) bewegen.
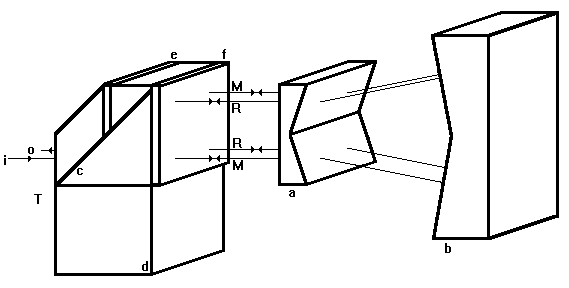
Bild 2.2.11: Anordnung zur Rollwinkelmessung, bestehend aus Doppelkeilprisma (a), Winkelspiegel (b), Strahlteiler (T) mit Polarisationsteilerschicht (c), Tripelprisma (d), l/2-Platte (e), l/4-Platte (f) und einfallendem (i) und austretendem (o) Strahl. Der Meß- bzw. Referenzstrahl ist mit M bzw. R bezeichnet.
Alternativ zur Anordnung nach Bild 2.2.10, in welcher zwei komplette Auswerteeinheiten erforderlich sind, besteht die Möglichkeit der Modifikation dieser Anordnung (Bild 2.2.11). Dazu wird die Anordnung des Bildes 2.2.7 unter Ersatz des Dachkantprismas (d in Bild 2.2.7) durch ein Tripelprisma (d in Bild 2.2.11) verwandt. Das hat zur Folge, daß der vorn unten vom Spiegel (b) erstmalig reflektierte Meßstrahl durch das Tripelprisma in die hinteren Ebene gelenkt wird und als oberer Strahl den Teiler (T) zur nochmaligen Reflexion am Spiegel (b) verläßt. Der Referenzstrahl verläuft analog. Dadurch kompensieren sich mögliche Verschiebungen des Keiles (a) während der Bewegung. Lediglich für rollende Bewegungen findet diese Kompensation nicht statt. Anzumerken bleibt, daß Messungen mit der Anordnung nach Bild 2.2.11 nur die halbe Auflösung (doppeltes Inkrement) gegenüber der Anordnung nach Bild 2.2.10 besitzen, daß nur eine Auswerteeinheit erforderlich ist, und daß die Lage der Drehachse nicht mehr ermittelt werden kann.
Auf mathematische Ableitungen zu den Rollwinkelmessungen soll hier und im folgenden verzichtet werden, da sie analog den Ableitungen zur Geradheitsmessung erfolgen können.
Eine andere mögliche Anordnung wurde in /19/ beschrieben, wobei dort die Trennung und Ablenkung der beiden orthogonalen Moden des einfallenden Laserbündels unter Verwendung eines Wollaston-Prismas /22/ anstelle der in Bild 2.2.11 verwandten Bauteile (a, c bis f) erfolgen. Diese Anordnung ist aber als problematisch einzuschätzen, da sie keine Vorsorgemaßnahmen gegen eine Rückkopplung des Laserbündels in den Resonator beinhaltet.
Ein von uns entwickeltes Interferometersystem, welches ebenfalls die Möglichkeit der Rollwinkelmessung bietet, soll im folgenden kurz aufgezeigt werden. Dazu wenden wir uns einführend dem Differentialspiegelinterferometer (Bild 2.2.12) zu, an dessen Aufbau die Funktionsweise des Teilerblocks erläutert werden soll.
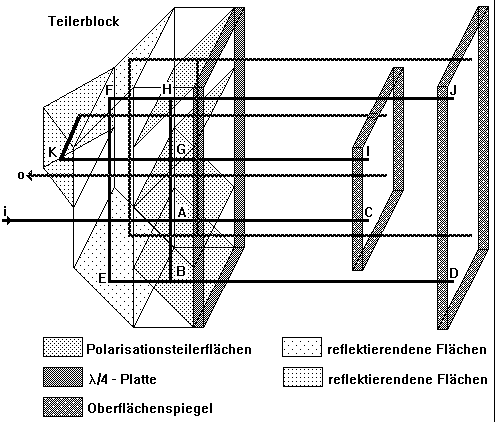
Bild 2.2.12: Differentialspiegelinterferometer mit achtfacher optischer Interpolation; es bezeichnen (i) den einfallenden und (o) den austretenden Strahl, die Großbuchstaben kennzeichnen einzelne Punkte der Anordnung.
Die beiden senkrecht zueinander polarisierten Moden des Inputstrahls (i) werden im Punkt A der Polarisationsteilerschicht getrennt. Eine Mode reflektiert und gelangt über die Punkte B - D - B - E - F - H - J - H zum Punkt G, die andere passiert die Polarisationsteilerschicht und erreicht über die Punkte C - A - G - I ebenfalls Punkt G. Dort vereinigen sich beide Moden, um - nachdem sie die Punkte K und K' (die gestrichenen Punkte liegen in der "hinteren" Ebene an der zu den ungestrichenen Größen äquivalenten Stelle) passiert haben - am Punkt G' wieder aufzuspalten. Über die Punkte H' - J' - H' - F' - E' - B' - D' - B' beziehungsweise I' - G' - A' - C' zum Punkt A' gelangend, vereinigen sie sich zum Outputstrahl, der das Interferometer in Richtung Auswerteeinheit verläßt. Da dabei alle reflektierenden Flächen mit Ausnahme der Oberflächenspiegel unter 45&#deg; zum ideal justierten Strahlengang stehen und symmetrisch zum mittigen Längs- bzw. Querschnitt des Interferometers stehen, kompensieren sie geringe Abweichungen der Meß- bzw. Referenzstrahlen vom Einfallslot der Oberflächenspiegel. Die Richtungen des In- und Outputstrahls sind deshalb bis auf das Vorzeichen identisch.
Der Interferometerblock ist ein Komplett-Bauteil (versprengt) und findet in allen Anordnungen dieser Anlage Verwendung. Zur besseren Übersichtlichkeit ist dieser Block in einigen, weiter unten aufgeführten Anordnungen etwas verzerrt abgebildet.
Durch die im Bild 2.2.13 gezeigte veränderte Anordnung der Spiegel läßt sich der in Bild 2.2.12 dargestellte Teilerblock als Nick- und Gierwinkelinterferometer einsetzen.
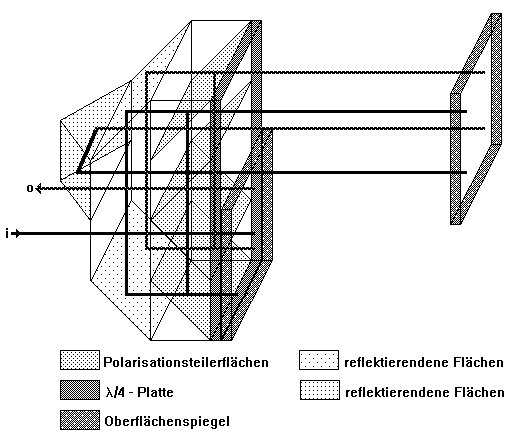
Bild 2.2.13: Nickwinkelinterferometer mit achtfacher optischer Interpolation; es bezeichnen (i) den einfallenden, (o) den austretenden Strahl
Das Nickwinkelinterferometer ist als Differentialspiegelinterferometer konzipiert. Das hat den Vorteil, daß der hier im Bild am Interferometerblock lokalisierte Referenzspiegel auch von diesem getrennt angeordnet sein kann, was zur Reduktion des Totwegfehlers sogar empfehlenswert ist. Zur Messung des Gierwinkels wird die gesamte im Bild 2.2.13 dargestellte Anordnung einfach um 90&#deg; gedreht.
Ersetzt man die im Bild 2.2.12 dargestellten Spiegel durch eine Prismen-Winkelspiegelkombination, dann erhält man die Möglichkeit der Messung der Geradheit (Bild 2.2.14) und des Rollwinkels (Bild 2.2.15). Der besseren Anschaulichkeit wegen sind die Anordnungen diese beiden Bilder etwas verzerrt dargestellt.
Der feststehende Winkelspiegel (Bild 2.2.14) dient als Geradheits- bzw. Rollwinkelachsennormal, wobei die Richtung der Normalgerade der Richtung des aus den beiden Flächennormalen bestehenden Summenvektors entspricht. Weicht der sich bewegende Doppelkeil von der Normalgeraden ab, so entstehen optische Wegdifferenzen zwischen den nach oben bzw. unten gerichteten Meß- bzw. Referenzstrahlen, die zur Geradheits- bzw. Rollwinkelabweichung proportional sind. Gegen Roll-, Nick- und Gierwinkelabweichungen ist das Geradheitsinterferometer invariant. Das Rollwinkelinterferometer ist gegen Geradheits-, Nick- und Gierwinkelabweichungen invariant.
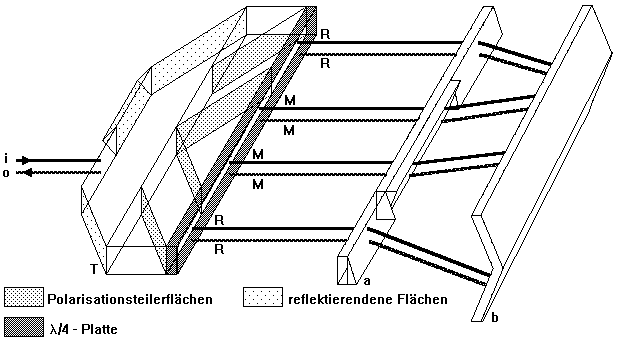
Bild 2.2.14: Geradheitsinterferometer mit achtfacher optischer Interpolation; (a) bezeichnet das Geradheitsprisma, (b) den Winkelspiegel,(T) den Strahlteilerblock, (i) den einfallenden und (o) den austretenden Strahl und (M) und (R) die Meß- und Referenzstrahlen
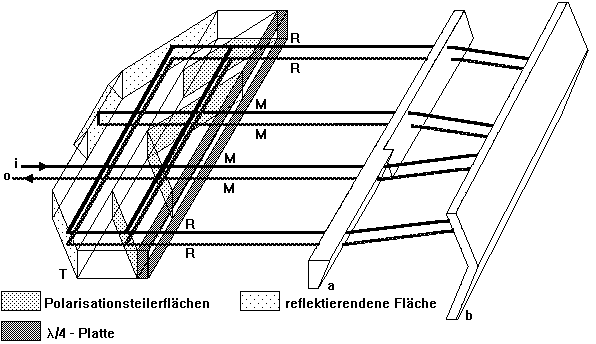
Bild 2.2.15: Rollwinkelinterferometer mit achtfacher optischer Interpolation; (a) bezeichnet das Geradheitsprisma, (b) den Winkelspiegel,(T) den Strahlteilerblock, (i) den einfallenden und (o) den austretenden Strahl und (M) und (R) die Meß- und Referenzstrahlen
Die Vorteile dieser beiden Anordnungen zur Rollwinkelmessung sind die doppelte Empfindlichkeit gegenüber der Anordnung nach Bild 2.2.7 und Bild 2.2.11 und die universelle Verwendbarkeit des Strahlteilerblocks zur Messung aller oben beschriebenen geometrischen Größen mit hoher Genauigkeit. Das in den Bildern 2.2.11 bis 2.2.12 dargestellte Interferometersystem ist nicht patentrechtlich geschützt.
Ein wesentlicher Nachteil der gesamten Anordnungen (Bilder 2.2.11 bis 2.2.15) besteht in der Komplexität des Strahlteilerblocks, dessen Teile hochgenau gefertigt und gekittet werden müssen, um die mögliche Meßgenauigkeit zu erreichen. Der Hauptnachteil sind aber die hohen, sich bei geringen Fertigungsstückzahlen nicht amortisierenden Herstellungskosten des Strahlteilerblocks. Außerdem erscheint eine rationelle Serienfertigung des dargestellten Strahlteilers problematisch. Deshalb sollen eine genauere Untersuchung der fehlerrelevanten Größen und eine mathematische Beschreibung entfallen.
Damit soll die für die nächsten Kapitel dienende Einführung in die Funktionsweise der Laserwegmeßsysteme und deren Meßanordnungen abgeschlossen werden.
Zur Realisierung qualitativ hochwertiger Messungen ist es unbedingt erforderlich, sich die eingehenden Meßfehler zu veranschaulichen und daraus resultierend Maßnahmen zu ihrer Minimierung abzuleiten. Weiterhin müssen den Anwendern des Laserwegmeßsystems die Grenzen der Meßgenauigkeit beziehungsweise die Vertrauensbereiche der Messungen angegeben werden. Diesen Aufgaben, dem eigentlichen Zweck der Diplomarbeit entsprechend, sollen die nächsten Kapitel gelten.
Die Vielzahl der möglichen Meßfehler läßt sich in fünf Gruppen einteilen.
Die erste Gruppe bilden die relativistischen Einflüsse. Hier seien
Eine zweite Gruppe stellen die Einflüsse der Umgebung wie
Als dritte Gruppe sind Fehler, die auf Grund des heterodynen und polarisationsorthogonalen Meßprinzips entstehen, wie zum Beispiel
Die aus dem Versuchsaufbau resultierenden Fehler wie
Eine fünfte Gruppe sind die technischen Fertigungstoleranzen, die den Meßwert über die in die Meßgleichungen eingehenden geometrischen Größen wie
Als ein weiteres Unterscheidungsmerkmal gilt die Unterteilung aller Meßfehler in konstante, von der Größe des Meßwertes unabhängige und in relative, von der Größe des Meßwertes abhängige Meßfehler. Diese Spezifikation ist leicht anhand der Angabe der Meßwerte (absolut oder pro Einheit des Meßwertes) zu treffen, sie soll daher hier nicht weiter verfolgt werden.
Im Laser auftretende Fehler werden ebenfalls nicht weiter diskutiert. Hier sollen die Toleranzangaben des Laserherstellers gelten. Grundlegende Untersuchungen zur von der Lasergeometrie, der Laserrohraufhängung, der Strahlaufweitung und thermischen Problemen beeinflußten Stabilität des Lasers finden sich in /28/.
Da die Wellenlänge l in alle Meßgleichungen linear eingeht, entsteht bei allen Meßprozessen der aus der Wellenlängenstabilität über die gesamte Lebensdauer /9/ resultierende Fehler
| (3.1.1) |
wobei X für den Wert der jeweils betrachteten Meßgröße steht. Die Stabilität der Wellenlänge bezieht sich dabei auf den (normalen) geregelten Betrieb des Lasers. In diesen Zusammenhang fiel bei Messungen, die während durchgeführten Preßlufthammerarbeiten in anderen Teilen des Gebäudes stattfanden, auf, daß sich diese auf die Stabilität der Laserwellenlänge auswirkten. Als Ursache kommen mechanische Schwingungen des Laserresonators in Betracht. Da solche Schwingungen evtl. auch in Werkhallen bei Maschinenabnahmen vorkommen könnten, müßte der Laser auf Empfindlichkeit hinsichtlich der Amplitude als auch der Stärke der Schwingungen untersucht werden. Dazu fehlten uns die Mittel und Möglichkeiten.
Ein weiterer Punkt ist die Abweichung der mit dem Lasermeßsystem ermittelten Geradheits- oder Ebenheitsabweichungen gegenüber solchen, die mit einem nach dem Gravitations- oder "Wasserwaagen"-Prinzip arbeitenden Meßsystem ermittelt wurden: Das "Wasserwaagen"-Prinzip arbeitet mit einem Normal, dessen Normalenvektor immer zum Erdmittelpunkt zeigt, und das deshalb letztlich einen Kreisbogen (bzw. eine Kugelfläche) beschreibt, während beim Laserwegmeßsystem die Gerade das Normal bildet. Die Differenz Dz zwischen beiden Normalen berechnet sich in Abhängigkeit vom zurückgelegten Weg x und dem Erdradius re nach
| (3.1.2) |
und beträgt auf einer Distanz von x = 10 m immerhin Dz » 8 mm.
Nach Kenntnisnahme dieser kurzen, über /29/ hinausgehenden Aufstellung soll es nun darum gehen, ausgewählte Fehler weiter zu konkretisieren. Dem wollen wir uns in den folgenden Kapiteln zuwenden und mit der Behandlung der Gruppe der relativistischen Fehler beginnen.
Durch die Wirkung der Gravitation werden die Photonen der Laserstrahlung beschleunigt, wobei sich ihre Wellenlänge ändert. Dieser Effekt resultiert aus der Veränderung der potentiellen Energie der Photonen im Schwerefeld der Erde, das im weiteren mit einer konstanten Erdbeschleunigung g vorausgesetzt werden soll. Die Photonen der Frequenz n besitzen eine Energie
| (3.2.1) |
und die relativistische Masse
| (3.2.2) |
Dabei bezeichnen h das Plancksche Wirkungsquantuum und co die Vakuumlichtgeschwindigkeit.
Im Schwerefeld der Erde besitzen die Photonen des Abstandes z von der Erdoberfläche eine potentielle Energie
| (3.2.3) |
Bewegt sich nun ein Photon mit nichtverschwindender z-Komponente der Geschwindigkeit (vz¹0), so ändert sich seine Energie entsprechend des Energieerhaltungssatzes
| (3.2.4) |
Dabei beziehen sich die Indizes 0 bzw. 1 auf Angaben vor bzw. nach dem Prozeß. Durch Einsetzten von (3.2.1) bis (3.2.3) in (3.2.4) ergibt sich
| (3.2.4a) |
beziehungsweise
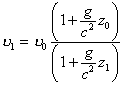 |
(3.2.5) |
Wegen c2 >> gz1 kann man den Nenner von Gl. (3.2.5) durch Reihenentwicklung unter Vernachlässigung aller in z1 nichtlinearen Glieder mit
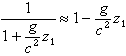 |
(3.2.6) |
nähern und erhält damit aus Gl. (3.2.5)
| (3.2.5a) |
bzw. nach Vernachlässigung aller in z nicht linearen Glieder
| (3.2.5b) |
Wegen c = ln folgt daraus
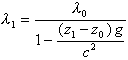 |
(3.2.7) |
Gl. (3.2.7) läßt sich durch Reihenentwicklung des Nenners unter Vernachlässigung aller in (z1 - z0) nicht linearen Glieder näherungsweise in
| (3.2.7a) |
oder unter Verwendung von Dl = l1 - l0 bzw. D z = z1 - z0 in
| (3.2.7b) |
umformen.
Durch Einsetzen der für das ZLM 300 zutreffenden mittleren Wellenlänge l0 = 632,8 nm in (3.2.6) erhält man
| (3.2.8) |
Die Änderung der Wellenlänge infolge der Gravitationsbeschleunigung der Photonen im konstant vorausgesetzten Gravitationsfeld ist daher ein für alle möglichen Messungen mit dem ZLM 300 zu vernachlässigender Prozeß.
Ein parallel zur Erdoberfläche in x-Richtung verlaufender Lichtstrahl ändert infolge des Gravitationsfeldes seine Ausbreitungsrichtung.
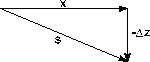
Bild 3.2.1: geometrischer Ansatz zur Bahnberechnung der Photonen im Schwerefeld, es bezeichnen x die unbeeinflußte Ausbreitung, Dz die Gravitationsablenkung und s die reale Ausbreitung der Photonen
Unter der Voraussetzung der Konstanz des Gravitationsfeldes und damit der Erdbeschleunigung g in der Nähe der Erdoberfläche kann man für den Weg
| (3.2.7b) |
| (3.2.9) |
den das Licht in der Zeit t zurücklegt,
| (3.2.9a) |
bzw. wegen x >> Dz näherungsweise
| (3.2.9b) |
ansetzen. Eliminiert man mit Hilfe von Gl. (3.2.9b) im Fallgesetz
| (3.2.10) |
Zeit t, dann erhält man die Gleichung
| (3.2.11) |
für die parabolische Photonenbahn im Erdschwerefeld, deren Lösung
| (3.2.12) |
beziehungsweise nach Umformung
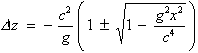 |
(3.2.12a) |
lautet. Entwickelt man nun die Wurzel der Gl. (3.2.12a) in eine Reihe und vernachlässigt alle höheren Glieder, so ergibt sich die klassisch-mechanische Wurfparabel für nichtrelativistische Geschwindigkeiten
| (3.2.12b) |
Die Korrektheit dieses Resultats wird in /30/ bestätigt. Setzt man in (3.2.12b) die erforderlichen Werte ein, dann ergibt sich der in Bild 3.2.2 angegebene Graph der Abweichung der Photonenbahn im Erdschwerefeld von der Gerade.
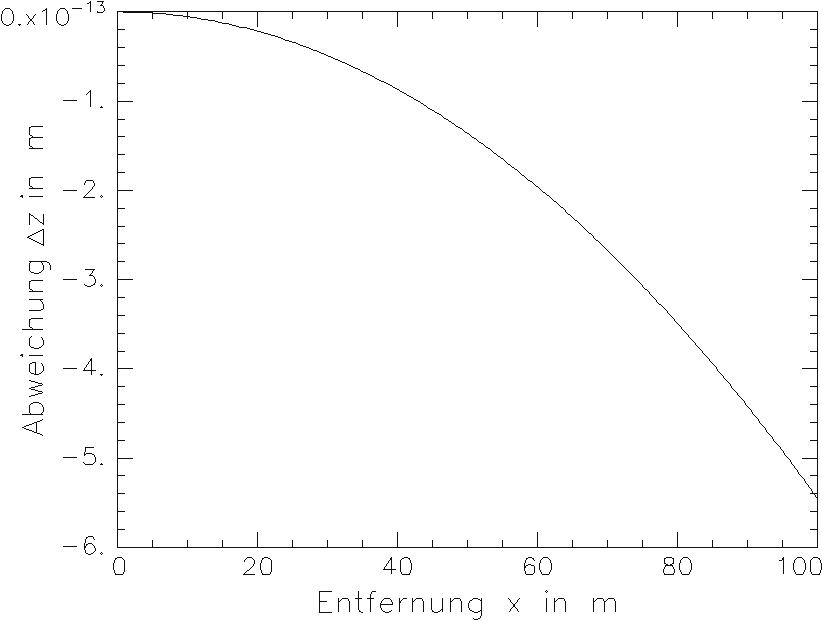
Bild 3.2.2: Vertikale Ablenkung Dz der Photonen im konstanten Erdschwerefeld in Abhängigkeit von der horizontalen Flugstrecke x
Wie man sich anhand der Werte der vorangehende Rechnung überzeugen kann, liegt die Abweichung des Laserstrahls von der Geraden bei horizontaler Lichtausbreitung über mit dem ZLM 300 zu messende Entfernungen von x £ 20 m um mehrere Größenordnungen unterhalb aller Inkremente und ist daher zu vernachlässigen.
Eine Überprüfung dieser Erkenntnis soll mit Hilfe einer Abschätzung der Strahlablenkung unter Zuhilfenahme von Ergebnissen der allgemeinen Relativitätstheorie erfolgen. Nach /31/ gilt für den Zusammenhang der Einsteinschen Gravitationskonstante c0 und der Newtonschen Gravitationskonstante g
| (3.2.13) |
für den Gravitationsradius rg eines Körpers bei homogen verteilter Ruhemasse m0
| (3.2.14) |
beziehungsweise
| (3.2.14a) |
und für den Ablenkwinkel Da eines Lichtstrahles, der diese Ruhemasse unter dem Abstand r0 zum Massenmittelpunkt passiert
| (3.2.15) |
Setzt man in die letzten beiden Gleichungen die Daten der Erde m = me = 5,98 x 1024 kg und r0 = re = 6,67 x 106 m , so erhält man für die Ablenkung Da eines Lichtstrahles an der Erde den Wert
| (3.2.16) |
Ein unter dem Winkel Da gegen die Horizontale verlaufender Strahl besitzt nach durchlaufener Strecke x die vertikale Abweichung z gegen die Horizontale
| (3.2.17) |
woraus unter Einsetzen von (3.2.16)
| (3.2.18) |
folgt. Die Geradheitsinkremente zink ergaben sich entsprechend den Gln. (2.2.23) und (2.2.24) zu zink,1 = 0,12 mm und zink,2 = 0,60 mm . Ein Vergleich dieser Wertes mit der aus (3.2.18) ermittelten Abweichung von z ( 20m ) » 5 nm zeigt, daß selbst dieser Wert um mehrere Größenordnungen unterhalb der Geradheitsinkremente liegt und damit vernachlässigt werden kann.
Ein weiterer relativistischer Einfluß ist der Dopplereffekt des Lichtes. Auf seiner Messung beruht letztlich das Meßprinzip des ZLM 300.
Der Dopplereffekt ist ursprünglich relativistischer Natur, es genügt jedoch meist, mit seiner nichtrelativistischen Näherung zu arbeiten. Bei hohen Genauigkeiten, wie sie letztlich vom hier zu behandelnden Laserwegmeßsystem erreicht werden, ist es jedoch erforderlich, die Verfälschungen dieser nichtrelativistischen Näherung zu ermitteln.
Durch den relativistischen, longitutinalen Dopplereffekt /32/ entsteht bei einer Relativgeschwindigkeit v zwischen Lichtquelle und Beobachter eine Verschiebung
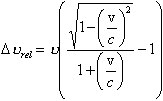 |
(3.2.19) |
der Lichtfrequenz n. Die Relativgeschwindigkeit v ist bei wachsender Entfernung zwischen Quelle und Beobachter positiv definiert. Durch Reihenentwicklung von Gl. (3.2.19) findet man die quadratische Näherung
| (3.2.20) |
Vergleicht man Gl. (3.2.14) mit der nichtrelativistischen, den Meßgleichungen zugrunde liegenden Dopplerverschiebung
| (3.2.21) |
ergibt sich als Differenz das quadratische Glied aus Gl. (3.2.20)
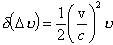 |
(3.2.22) |
Diese näherungsbedingte Frequenzabweichung entspricht unter Berücksichtigung der Frequenzänderung (3.2.21) des nichtrelativistischen Dopplereffekts einem relativen Frequenzfehler von
| (3.2.23) |
Entsprechend den Gl. (2.1.10) und (2.1.8c) setzt sich der Fehler (2.3.23) linear fort, das heißt, es gilt nach
| (3.2.24) |
für den daraus resultierenden Wegfehler
| (3.2.25) |
Durch Einsetzen der für das ZLM 300 zulässigen Maximalgeschwindigkeit vmax des Meßprismas ((b) in Bild 2.1.1) von vmax = 6,33 ms-1 erhält man
| (3.2.26) |
woraus sich unter Nutzung der maximalen Meßentfernung /33/ von x = 20 m eine maximale mögliche Verfälschung der Meßergebnisse von Dx = 22 nm ergibt. Dieses Ergebnis gilt ebenfalls für Meßanordnungen mit höherer optischer Interpolation, da sich die maximal zulässige Geschwindigkeit des Meßreflektors entsprechend verringert.
Der Meßfehler (2.3.18) liegt in der Größenordnung der Auflösung des Systems. Er muß, wie sich in späteren Kapiteln noch zeigen wird, bei der Messung in Luft nicht berücksichtigt werden, da dann die atmosphärischen Einflüsse einen wesentlich größeren Fehler erzeugen. Bei den Winkelmessungen und bei den Messungen der Geradheit kann man Gl. (2.3.18) vollständig vernachlässigen, da der dabei mögliche Meßbereich durch Gl. (2.2.2) mit sina < 1 bzw. Gl. (2.2.17) mit zg < ± 2 mm wesentlich beschränkter ist.
Die Fehler infolge des Einflusses der Atmosphäre bilden eine Hauptgruppe der auf die Messung einwirkenden Fehler. Deshalb bedürfen sie einer gründlichen Betrachtung.
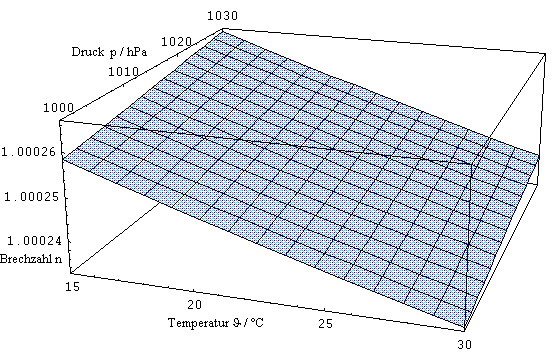
Nach Untersuchungen von Edlén /34/ sowie Birch und Downs /35/ wirken sich die Umwelteinflüsse unmittelbar auf die Brechzahl der Luft aus. Wichtigste Einflußfaktoren sind die Temperatur J, der Druck p und die Luftfeuchte, die hier in ihrer relativen Angabe FR verwendet werden soll. Für die Vakuumwellenlänge l0
| (3.3.1) |
von diesen Parametern ab, wobei der Luftdruck in hPa, die relative Luftfeuchte in % und die Temperatur in &#deg;C angegeben ist. Diese Angabe ist in Bild 3.3.1 dargestellt und bezieht sich auf "Standartluft" /36/, einer definierten Zusammensetzung der Luft aus ihren Bestandteilen.
Nach
| (3.3.2) |
hängt die Luftwellenlänge l von der Luftbrechzahl nl und der Vakuumwellenlänge l0 ab. Bei Messungen in Luft muß selbstverständlich diese Wellenlänge in den Meßgleichungen (2.1.8d; 2.2.5; 2.2.18) verwandt werden. Es ergeben sich die Gleichungen ( alles Planspiegelvarianten, daher ohne Indizes P)
| (3.3.3) | |
| (3.3.4) | |
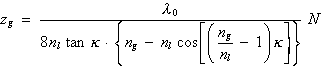 |
(3.3.5) |
für die Zusammenhänge des Weges x, des Winkels a und der Geradheitsabweichung zg mit den Zählwerten. Die Kompensation der Luftwellenlänge kann also unter Zuhilfenahme der Formel (3.3.1) in den Meßgleichungen (3.3.3) - (3.3.5) erfolgen. Umwelteinflüsse wirken sich dann nur noch als Folge der Meßungenauigkeiten der Werte für Druck, Temperatur und Luftfeuchte aus.
Zur Berücksichtigung der Umweltbedingungen ist es erforderlich, der Auswerteeinheit mit PC diese Parameterwerte mitzuteilen. Das kann beispielsweise durch Eingabe der Daten von Hand geschehen. Dabei kann man von einer Genauigkeit der Parameter von
bei durchschnittlichen Werkstattbedingungen mit
ausgehen. Aus
| (3.3.6) |
beziehungsweise
| (3.3.7) |
und den maximalen Brechzahlfehler
| (3.3.8) | |
| (3.3.8a) | |
| (3.3.8b) |
folgt als Größtfehler des Weges
| (3.3.9) |
Analog ergibt sich für die Winkelmessung der Größtfehler
| (3.3.10) |
Der Größtfehler der Geradheitsmessung ermittelt sich zu
| (3.3.11) |
bzw. unter Berücksichtigung von Gl. (3.3.5) zu
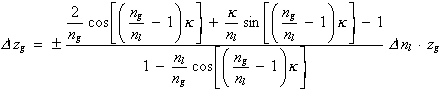 |
(3.3.11a) |
woraus nach Einsetzen von ng, nl undk entsprechend Kap. 2.2.3
| (3.3.11b) | |
| (3.3.11c) |
folgt. Dabei gilt Gl. (3.3.11b) für Messungen mit dem Doppelkeilprisma 1 und Gl. (3.3.11c) für Messungen mit dem Doppelkeilprisma 2 (vgl. Kapitel 2.2.3). Bei aus der technischen Realisierung bedingten, maximal meßbaren Geradheitsabweichungen von zg < ± 2 mm und Dn < 10-5 ergibt sich der maximale Fehler
| (3.3.12) |
deren weit unter den Inkrementen Gl. (2.2.23) und (2.2.24) liegender Betrag im Sinne der aus der Brechzahlunsicherheit (3.3.8b) bzw. der statistischen Schwankungen der Luftbrechzahl (Kap. 3.4 und Kap. 4) folgenden Geradheitsmeßunsicherheit nicht berücksichtigt werden muß. Eine gänzliche Vernachlässigung (n=1) der Luftbrechzahl in Gl. (3.3.5) ist jedoch nicht möglich.
Um die Fehler der Längen- und Winkelmessung reduzieren zu können, wurde von Chour und Hecht, Carl Zeiss Jena GmbH, ein automatischer Umweltkompensator /37/ geschaffen, der mit einer Rate von je einem Meßwert pro Sekunde die in Gl. (3.3.1) eingehenden Parameter Luftdruck, -temperatur und relative Luftfeuchte sowie die Prüflingstemperatur an fünf wählbaren Punkten mit Meßunsicherheiten von
innerhalb der werkstattüblichen Wertebereiche ermittelt. Unter Verwendung dieser und der weiter oben genannten Werkstattbedingungen ergeben sich aus den Gln. (3.3.6) - (3.3.8) und (3.3.11) die Meßunsicherheiten
| (3.3.13) | |
|
(3.3.14) |
Eine weitere Senkung der Meßunsicherheit läßt sich durch direkte Messung der Wellenlänge mittels Wellenlängen-Verfolgern (Wavelength-Tracker) oder Refraktometern erzielen. Erreichbare Meßunsicherheiten geben Hewlett-Packard (Tracker, HP10717A) mit 1,0x107 /29/ bzw. 1,5x10-7 /38/, Spindler & Hoyer (Refraktometer LR1) mit 5x10-7 /39/ und Zygo mit 3,8x10-9 /40/ an. Der ökonomische Aufwand hierfür ist allerdings hoch (zweites Interferometer), so daß sich der Einsatz solcher Geräte nur für wenige, spezielle Aufgaben lohnt. Auch Messungen unter genau definierten Meßraumbedingungen auf Grundlage der Brechzahlberechnung aus den Parametern erlauben Meßunsicherheiten kleiner 10-6 /26/.
Nach Abhandlung dieses grundlegenden Punktes wollen wir uns nun den Untersuchungen der einzelnen Umwelteinflüsse zuwenden. Erster Untersuchungsgegenstand soll dabei der Einfluß der Extinktion des Laserlichts auf das Meßergebnis sein
Bei der Ausbreitung des Laserliches, die in x-Richtung erfolgen soll, findet eine Abnahme der Intensität statt. Anstelle der Intensität I soll aber der an den Empfängerdioden die Leistung P erzeugende Strahlungsfluß F
| (3.3.15) |
betrachtet werden, da er über die Linsen (L in Bild 2.1.2) der Querschnittsfläche F in die Lichtleitfasern eingekoppelt und den Empfängerdioden zugeführt wird. Unter Vernachlässigung der in bei der Integration über die Fläche F eingehenden Strahldivergenz des Laserstrahls kann man in Analogie zu der Intensitätsbetrachtung voraussetzen, daß der den Laser am Ort x = 0 verlassende Strahlungsfluß infolge der Absorption mit dem Absorptionskoeffizienten aA und der Streuung mit dem Streukoeffizienten aS pro Wegelement um
| (3.3.16) |
verringert wird. Die beiden Koeffizienten aA und aS lassen sich zum Extinktionskoeffizienten aE zusammenfassen. Durch Integration von (3.3.16) ergibt sich
| (3.3.17) |
Hierin bezeichnet F0 den den Laser verlassenden Strahlungsfluß. Die Extinktionskoeffizienten für Luft liegen nach /41/ in der Größenordnung aE = (0,001...0,1) m-1.
Bei Betrachtung der mit dem ZLM 300 zulässigen maximalen Meßentfernung von x = 20 m ergibt sich ein maximaler Strahlungsflußabfall von
| (3.3.18) |
Da das ZLM 300 konstruktiv für einen Strahlungsfluß bis
| (3.3.19) |
ausgelegt ist, muß die Absorption und Streuung der Atmosphäre nicht berücksichtigt werden.
Zur Vereinfachung der Berechnung der Abhandlungen wollen wir uns auf eine zweidimensionale Temperaturverteilung der Form
| (3.3.20) |
mit konstantem Gradienten
| (3.3.21) |
zurückziehen. Die x-z-Ebene (Bild 3.3.2) wird dabei durch die Schnittebene der Strahlausbreitung und des dazu unter dem Winkel stehenden Temperaturgradienten definiert, wobei die x-Achse mit der Ausbreitungsrichtung des Laserstrahls im Nullpunkt identisch ist.
Verursacht durch die wegen des Temperaturgradienten vorhandene Brechzahlveränderung erfährt der sich ausbreitende Laserstrahl eine geringe Ablenkung, er breitet sich nicht mehr geradlinig aus. Die Abweichung der Ausbreitung des Laserlichtes von der Geraden soll im folgenden berechnet werden.
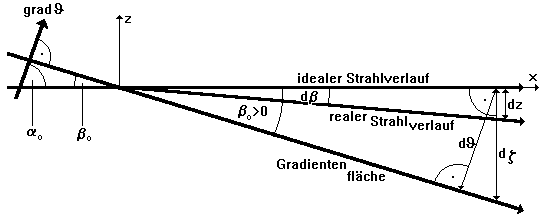
Bild 3.3.2: Strahlausbreitung unter dem Einfluß eines Temperaturgradienten; es bezeichnen
J die Temperatur, a0 bzw. b0 die Winkel des Strahls gegen den Temperaturgradienten bzw. die Temperaturschichtung bei Eintritt des Strahls in das inhomogene Temperaturfeld, dJ die Temperaturveränderung in der Umgebung des Strahles während seiner Ausbreitung im inhomogenen Temperaturfeld und db bzw. dz die Abweichung des Strahles von seiner ursprünglichen Richtung bzw. Ausbreitungsrichtung als Folge der Einwirkung des inhomogenen Temperaturfeldes.
Nach Sommerfeld /42/ kann man für ein Medium mit paralleler Brechzahlschichtung das Brechungsgesetz in der Form
| sin a = const. | (3.3.22) |
verwenden. Danach hat der Laserstrahl im Punkt P(x, y) die Strahlrichtung
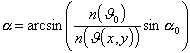 |
(3.3.23) |
Zur Ermittlung der Abweichung des Laserstrahls Dz von der Geraden soll das Brechungsgesetz in seiner differentiellen Form betrachtet werden. Aus Gl. (3.3.22) folgt
| (3.3.22a) |
Durch Differentiation erhält man
| (3.3.24) | |
| (3.3.24a) |
wobei infolge der Verwendung der Ableitung der Umkehrfunktion (3.3.22a) von Gl. (3.3.23) a0 ¹ 0 zu fordern ist /43/. Wegen tan a = cot b und da = -db (Bild 3.3.2) folgt
| (3.3.24b) |
Nach Bild 3.3.2 gilt weiterhin
| (3.3.25) |
woraus unter Einsetzen von Gl. (3.3.24b)
| (3.3.25a) |
folgt. Unter Nutzung des totalen Differentials (der Druck p soll konstant sein)
| (3.3.26) |
ergibt sich
| (3.3.25b) |
Entsprechend Bild 3.3.2 ist
| (3.3.28) | |
| (3.3.28a) |
weshalb aus Gl. (3.3.25b)
| (3.3.25c) |
folgt. Integriert man jetzt über die Ausbreitungsrichtung des Strahles vom Koordinatenursprung zum Punkt P(x, 0) (Bild 3.3.2)
| (3.3.29) |
und vernachlässigt die Änderung der Brechzahl längs des Weges
| (3.3.29a) |
dann ergibt sich
| (3.3.30) |
Der durch den Temperaturgradienten verursachte Gradient dn/dJ der Brechzahl in Gl. (3.3.30) wird nicht durch die Ableitung von Gl. (3.3.1), sondern durch die der vereinfachten Edlén-Gleichung /36/
| (3.3.31) |
eliminiert. Dies ist zulässig, da der Druck und die Luftfeuchte konstant sind, und die Temperaturänderung gering ist. Unter Berücksichtigung der Ableitung von Gl. (3.3.31)
| (3.3.32) |
erhält man aus Gl. (3.3.30) unter normalen Werkstatt-Umweltbedingungen
| (3.3.30a) |
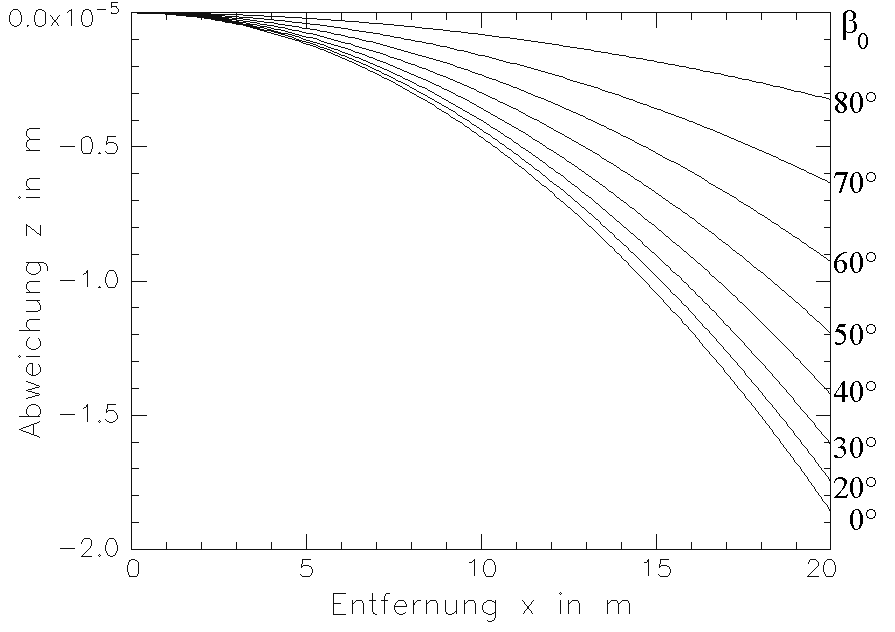
Eine grafische Darstellung des Zusammenhanges für ½grad J½ = 0,1 °C/m zeigt Bild 3.3.3.
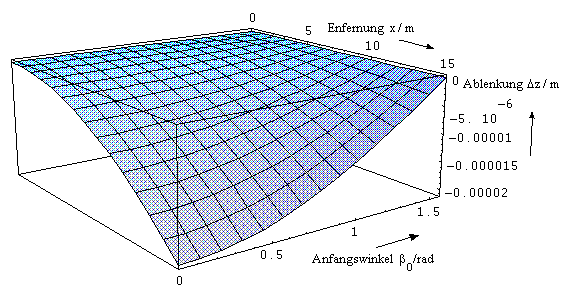
Untersucht man Gl. (3.3.30) näher, so ergibt sich eine maximale Abweichung für b0 = 0, obwohl sich für b0 = 0 die Temperatur, damit die Brechzahl und damit nach dem Brechungsgesetz die Ausbreitungsrichtung nicht ändern.
Eine Betrachtung der Grenzwerte der Gl. (3.3.25c) für b ® ± 0 zeigt, daß es sich bei b0 = 0 um eine sogenannte hebbare Unstetigkeitsstelle handelt, eine Integration darüber hinweg ist mathematisch zulässig. Da aber nach dem zugrundeliegenden Brechungsgesetz die Ablenkung db für b = 0 wegen n = const. zum Erliegen kommen muß, bedarf dieser Punkt einer besonderen Untersuchung.
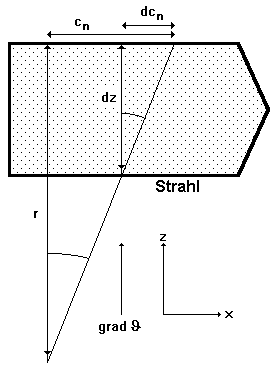 |
Bild 3.3.4: Der Laserstrahl als ausgedehntes Objekt; es bezeichnen grad J den konstanten Temperaturgradienten, cn die Lichtgeschwindigkeit in der jeweiligen Temperaturschicht, dcn die Änderung der Lichtgeschwindigkeit über der Schichtdicke dz der Temperaturschicht und r den Krümmungsradius der Strahlablenkung |
Betrachten wir nun den Fall der Lichtausbreitung parallel zur Brechzahlschichtung (b=0). Da sich in diesem Fall die Brechzahl nicht ändert, kann diese Betrachtung nicht auf der Grundlage des Brechungsgesetzes ausgeführt werden. Betrachten wir daher den Strahl als ein vom Querschnitt her ausgedehntes Objekt (Bild 3.3.4). Die Phasengeschwindigkeit in den optisch dünneren Teilen der Atmosphäre ist größer als die in den optisch dichteren Schichten. Durch die über den Strahlquerschnitt stetig veränderliche Phasengeschwindigkeit kommt es deshalb zu einer Abweichung der Ausbreitung des Strahles von der Geraden. Diese Strahlkrümmung muß gleichzeitig ein Überschreiten der Unstetigkeitsstelle nach Gl. (3.3.25c) bewirken, so daß diese nicht weiter beachtet werden muß. Nach Bild 3.3.4 ergibt sich der Zusammenhang zwischen der Lichtgeschwindigkeit c, ihrer Ableitung nach dem Ort dc/dz und dem Krümmungsradius r des Strahles
| (3.3.33) |
Die Abhängigkeit der Phasengeschwindigkeit der des Lichtes von Brechzahl eines Mediums
| (3.3.34) |
soll in differentieller Form
| (3.3.35) |
in Gl. (3.3.33) berücksichtigt werden. Es ergibt sich
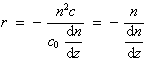 |
(3.3.36) |
Zur Substitution von dn nutzt man
| (3.3.26) |
und erhält
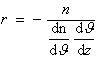 |
(3.3.36a) |
Für b = 0 (Bild 3.3.2) ist aber gerade
| (3.3.37) |
so daß sich der Krümmungsradius r zu
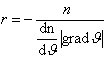 |
(3.3.36b) |
ergibt.
Unter Nutzung der Gl. (3.3.32), unserer Werkstattbedingungen
und n » 1 erhält man einen Krümmungsradius von r = 10 770 km.
Betrachtet man nun Gl. (3.3.30) im Grenzwert b ® 0, so muß man eine Übereinstimmung mit (3.3.36b) erwarten, da letztlich beide Gleichungen auf der Gültigkeit des Huygensschen Prinzips beruhen. Dazu bildet man in (3.3.30) den Grenzwert
| (3.3.38) |
und berechnet den Krümmungsradius im Punk x = 0 (vgl. Bild 3.3.2). Nach /43/ berechnet sich die Krümmung entsprechend
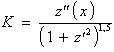 |
(3.3.39) |
Daraus ergibt sich der Krümmungsradius
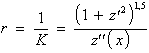 |
(3.3.40) |
Die Ableitungen von (3.3.30) an der Stelle x = 0 sind
| (3.3.41) |
| (3.3.42) |
und der Krümmungsradius ergibt sich daraus zu
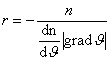 |
(3.3.43) |
Dies stimmt mit Gl. (3.3.36b) überein. Damit ist bewiesen, daß Gl. (3.3.30) exakt in b0 = 0 gilt. Die Gültigkeit der Gl. (3.3.30) bedarf damit bezüglich des Anfangswinkels b0 keinerlei Einschränkungen.
Abschließend (Bild 3.3.5) erfolgt nochmals eine graphische Darstellung der durch Gl. (3.3.30) beschriebenen Abweichung.
Im Kapitel 3.3.2 wurde bereits die Extinktion elektromagnetischer Wellen in der Atmosphäre behandelt. Durch Ausschluß der Streuung aus den Betrachtungen aS = 0 geht Gl. (3.3.17) in
| (3.3.44) |
über. Diese Leistung wird absorbiert und führt zu einer Erwärmung der Atmosphäre längs des Strahles. Das wiederum führt, wenn man den Strahl als ausgedehntes Objekt betrachtet, zu Verfälschungen des Intensitätsprofils des Strahls (Bild 3.3.6).
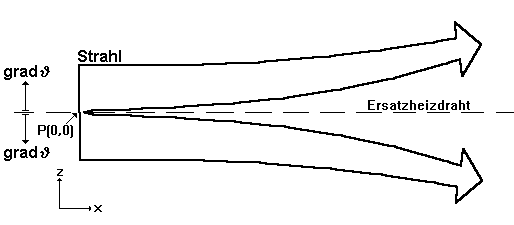
Bild 3.3.6: Schema der Eigendefokussierung des Laserstrahlen
Schüßler /41/ behandelt dieses Problem näherungsweise, indem er die durch Absorption erzeugte thermische Energie ersatzweise durch einen eindimensionalen (elektrischen) Heizdraht zuführt. Längs dessen breitet sich der betrachtete Laserstrahl absorptionslos aus. Dabei kommt es infolge der Temperaturverteilung zur Ablenkung Dz der einzelnen Strahlanteile des Anfangsabstandes z0
| (3.3.45) | |
| (P0 in mW, Strahlmitte Û z0 = 0) | |
Eine grafische Darstellung für eine Anfangsleistung P0 = 1 mW zeigt Bild 3.3.7.
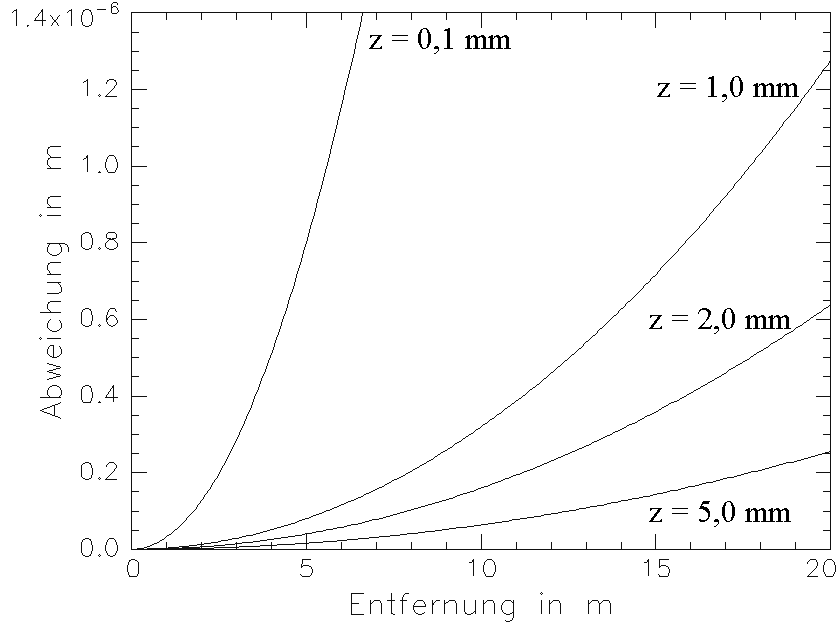
Bild 3.3.7: Ablenkung für Strahlanteile verschiedener Abstände z von der Strahlmittelachse z = 0 als Funktion der vom Strahl zurückgelegten Entfernung
Im Bild 3.3.7 erkennt man, daß symmetrieachsennahe Strahlanteile eine stärkere Ablenkung erfahren als achsferne. Das führt zu einer geringen Strahlaufweitung und einer kegelförmigen "Aushöhlung" des Strahles längs seiner Symmetrieachse. Bild 3.3.7 veranschaulicht diesen Effekt qualitativ. Unter Berücksichtigung der Tatsache, daß diese Abweichungen unterhalb des Promill-Bereiches des Strahlradius liegen und daß - durch die Mittelung der hinreichend großen Empfängerdioden über ihre Fläche bedingt - kein Energieverlust eintritt, bedarf der Einfluß der thermischen Eigendefokussierung keiner Berücksichtigung. Die zur Ermittlung der Parameter des Gauß’schen Bündels (in Kap. 1.3) durchgeführten Messungen zeigten diese Veränderungen des Strahlprofils nicht. Das begründet sich in den statistischen Einflüssen der Atmosphäre (vgl. Kap. 3.4), die diesen Effekt bis zur Nichtmeßbarkeit verzerrten. Eine genauere theoretische Beschreibung der thermischen Eigendefokussierung findet sich in /44/.
Der Luftdruck übt, da er in der Edlén-Gleichung (3.3.31) neben der Temperatur als Parameter auftritt, ebenfalls einen Einfluß auf die Ausbreitung des Laserstrahls aus. Dieser Einfluß ist Gegenstand der folgenden Untersuchung.
Zur Vereinfachung der Betrachtungen soll in Analogie zu den Betrachtungen des Kapitels 3.3.3 eine zweidimensionale Druckverteilung der Form
| (3.3.43) |
mit konstantem Gradienten
| (3.3.21a) |
betrachtet werden. Die x-z-Ebene (Bild 3.3.8) wird dabei durch die Schnittebene der Strahlausbreitung und des dazu unter dem Winkel a stehenden Druckgradienten definiert, wobei die x-Achse mit der Ausbreitungsrichtung des Laserstrahls im Nullpunkt identisch ist.
Verursacht durch die wegen des Druckgradienten vorhandene Brechzahlveränderung erfährt der sich ausbreitende Laserstrahl eine geringe Ablenkung, er breitet sich nicht mehr geradlinig aus. Der Ansatz kann in gleicher Weise zu Kapitel 3.3.3.1 erfolgen (Bild 3.3.8).
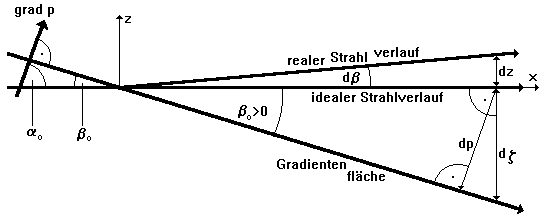
Bild 3.3.8: Strahlausbreitung unter dem Einfluß eines Druckgradienten, besondere Beachtung gebührt der in Vergleich zum Bild 3.3.2 entgegengesetzt gerichteten Ablenkung des Strahles; es bezeichnen p die Temperatur, a0 bzw. b0 die Winkel des Strahls gegen den Druckgradienten bzw. die Druckschichtung bei Eintritt des Strahls in das inhomogene Temperaturfeld, dp die Temperaturveränderung in der Umgebung des Strahles während seiner Ausbreitung im inhomogenen Druckfeld und db bzw. dz die Abweichung des Strahles von seiner ursprünglichen Richtung bzw. Ausbreitungsrichtung als Folge der Einwirkung des inhomogenen Druckfeldes
Da die dazu erforderlichen Betrachtungen mit denen des vorangegangenen Kapitels prinzipiell übereinstimmen, werden hier lediglich die Unterschiede dazu dargelegt: Gl. (3.3.26) ersetzt man unter der Forderung T = const. durch
| (3.3.46) |
und daraus resultierend Gl. (3.3.28a) durch
| (3.3.47) |
Dann ergibt sich völlig analog zu (3.3.30) die Abweichung
| (3.3.48) |
Die zu den im Kapitel 3.3.3.1 entgegengesetzte Ablenkrichtung ergibt sich aus der aus Gl. (3.3.31) folgenden Ableitung
| (3.3.49) |
deren Vorzeichen von dem der Ableitung (3.3.32) abweicht. Unter Nutzung der Umwelttemperatur J = 20 &#deg;C und n » 1 erhält man
| (3.3.49a) |
woraus
| (3.3.48a) |
folgt. Die Darstellung der im Falle b ® 0 maximal werdenden Geradheitsabweichung zeigt Bild 3.3.9.
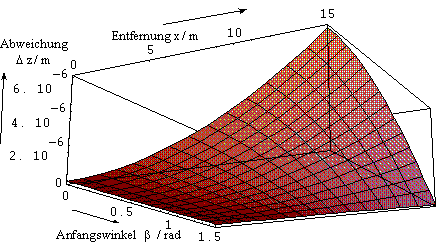
Bild 3.3.9: Darstellung der Abweichung von der geradlinigen Ausbreitung Dz als Funktion des Anfangswinkels b und der Entfernung x vom Anfangspunkt (Gl. (3.3.48a)) für einen Druckgradienten von 0,1 hPa/m
Einen Spezialfall der Gl. (3.3.48a) bildet die Geradheitsabweichung, die auf dem Vorhandensein des natürlichen, gravitationsbedingten Druckgradienten beruht. Dazu setzt man als Druckgradienten die Ableitung der Barometrischen Höhenformel grad p = -rg (r...Dichte der Luft /45/) und erhält
| (3.3.48b) |
für 20 &#deg;C, wobei b0 jetzt den Winkel zur Horizontalen beschreibt.
Ein weiterer Einflußfaktor sind Druckwellen, wie z.B. Schall. Schall ist physikalisch gesehen eine Wellenerscheinung des Druckes, wobei letztlich die verschiedensten Geräusche aus Fourierreihen der Grundschwingungen und ihrer Harmonischen zusammengesetzt sind. Die Betrachtung der daraus resultierenden Abweichungen soll hier nur für eine rein sinusförmige Welle erfolgen (Bild 3.3.10).
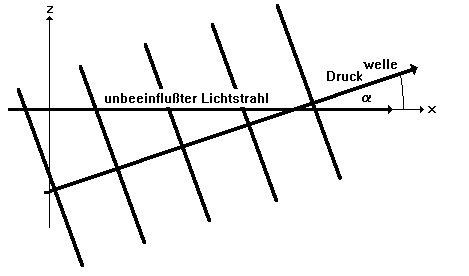
Der Schallpegel Ps von Industriegeräuschen liegt nach /46/ meist zwischen 80...100 dB, das Frequenzband umfaßt Geräusche der Frequenz n < 4 kHz. Dies entspricht gemäß der Definition des Bel bezüglich der Amplitude des Druckes p
| (3.3.50) |
und der international festgelegten Hörschwelle (bei n = 1 kHz) von
| (3.3.51) |
einer Druckwelle (Schwankung um Mittelwert p)
| (3.3.52) |
der Kreisfrequenz w mit dem Wellenzahlvektor
| (3.3.52a) |
am Ort
| (3.3.52b) |
Die senkrecht auf der Gerade z = 0 stehende z-Komponente des Druckgradienten ergibt sich durch Differentiation von Gl. (3.3.52) nach z an der Stelle z = 0 zu
| (3.3.53) |
Sie verursacht eine Geradheitsabweichung des Laserstrahls von der mit der x-Achse identischen unbeeinflußten Ausbreitungsrichtung. Diese berechnet sich gemäß dem für den Druck geltenden Analogon zu Gl. (3.3.29)
| (3.3.29b) |
Unter Verwendung der aus Bild 3.3.8 ablesbaren Beziehung
| (3.3.54) |
der Gl. (3.3.49a) und n0 » 1 erhält man die resultierende Geradheitsabweichung
| (3.3.55) |
Wegen der Unübersichtlichkeit der allgemeinen Lösung des Integrals der Gl. (3.3.55) soll diese nur für den Spezialfall a = 90&#deg; angegeben werden. In diesem Fall steht der Druckgradient senkrecht auf der Ausbreitungsrichtung des Laserstrahls, was, wie in vorhergehenden Kapitel gezeigt, dem Fall der Maximalablenkung des Laserstrahls entspricht. Gl. (3.3.55) vereinfacht sich zu
| (3.3.55a) |
die Lösung
| (3.3.55b) |
stimmt mit /41/ überein.
Unter Verwendung der von der für Werkstattbedingungen gültigen Schallgeschwindigkeit cs = 343 m/s abhängigen Beziehung ks = ws / cs folgt
| (3.3.56) |
Wie Gl. (3.3.56) zeigt, ist die Geradheitsabweichung zeitabhängig. Der Laserstrahl schwingt in der Frequenz der verursachenden Druckwelle und mit entfernungsabhängiger Amplitude um seine ungestörte Lage, die Schwingung findet in der Ebene der Ausbreitungsrichtung und des Wellenzahlvektors statt. Eine Darstellung der Amplitude zeigt Bild 3.3.11.
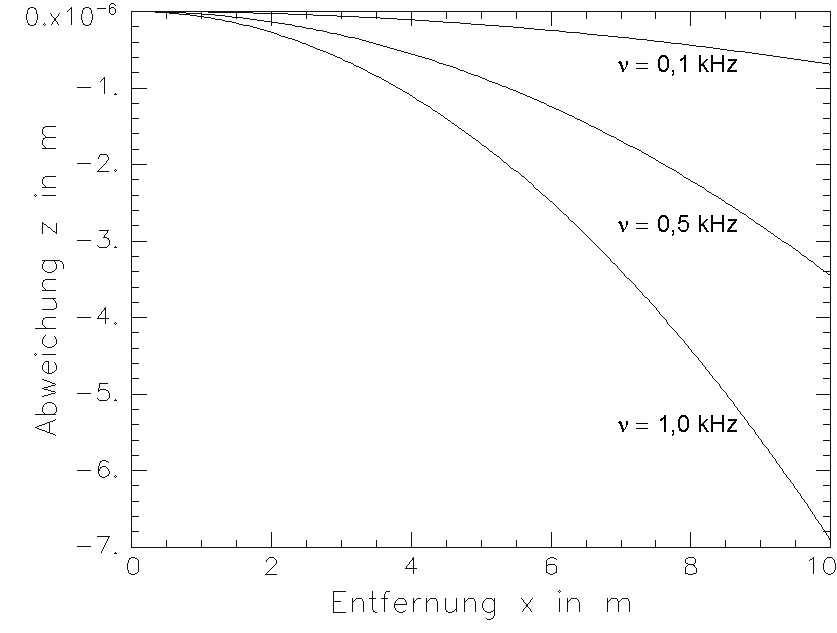
Bild 3.3.11: Darstellung der Amplitude der Geradheitsabweichung eines Laserstrahls, verursacht durch eine sich senkrecht zum Laserstrahl ausbreitende ebene Schallwelle des Schallpegels 100 dB für verschiedene Schallfrequenzen n
Die x-Komponente der Druckwelle (3.3.52) schwankt um ihren Mittelwert p0 nach
| (3.3.57) |
und verursacht dadurch eine periodische Änderung der Brechzahl und damit der gemessenen Weglänge x
| (3.3.58) | |
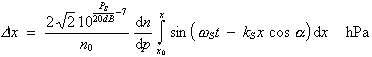 |
(3.3.58a) |
Das Ausführen der Integration mit x0 = 0 ergibt
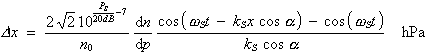 |
(3.3.59) |
Die durch den Term ks x cos a erzeugte Phasendifferenz beider Cosini moduliert den Entfernungsmeßwert.
Im Grenzfall a ® 0 erfolgt diese Modulation unmittelbar mit der Wellenzahl ks . Im Grenzfall a ® p / 2 ergibt sich aus Gl. (3.3.59) unter Verwendung der Regel von de l'Hospital
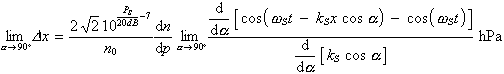 |
(3.3.60) |
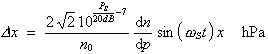 |
(3.3.60a) |
Die Amplitude von Gl. (3.3.60a) besitzt unter Werkstattbedingungen die Größe
| (3.3.60b) |
Der Entfernungsmeßwert schwingt mit frequenzunabhängiger, wohl aber schallpegelabhängiger Amplitude (3.3.60b) in der Frequenz der verursachenden Druckwelle um seinen ungestörten Wert. Eine Darstellung der Amplitude zeigt Bild 3.3.12.
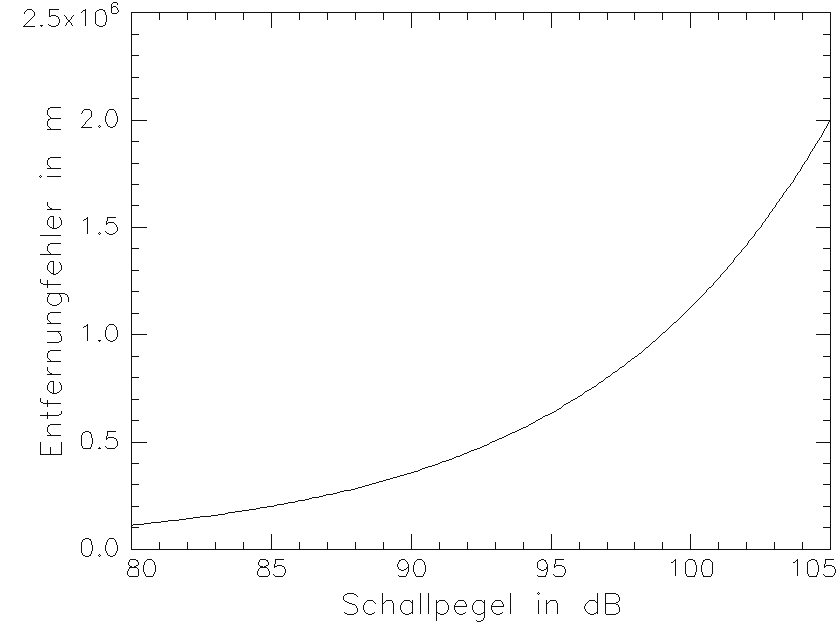
Bild 3.3.12: Amplitude des Entfernungsmeßfehlers in Abhängigkeit vom Schallpegels für eine sich senkrecht zum Strahl ausbreitende ebene Schallwelle bei einer Meßentfernung von x = 1,50 m
Da die in den Kap. 3.3.3 und 3.3.4 besprochenen Abweichungen gemeinsam auftreten, müssen sie zusammengefaßt werden. Wegen der Einschränkung der Betrachtungen der vorangegangenen Kapitel auf die Strahl-Gradienten-Ebene ist dabei zu beachten, daß diese Ebenen für Druck bzw. Temperatur im allgemeinen nicht übereinstimmen. Deshalb betrachten wir die Abweichungen als Vektoren, deren Richtung mit der Richtung der Projektion der jeweiligen Gradienten auf eine senkrecht zur idealen Strahlrichtung stehenden Ebene übereinstimmt. Diese Abweichungen kann man vektoriell oder unter Nutzung ihrer Beträge nach dem Cosinussatz
| (3.3.61) |
addieren. Bezogen auf den hier diskutierten Fall identifiziert man a mit der durch den Temperaturgradienten bedingten Abweichung (3.3.30) und b mit der durch den Druckgradienten bedingten Abweichung (3.3.48). Der Winkel g ist dann der Winkel zwischen der Richtung des Temperaturgradienten und der Richtung des Druckgradienten in der oben genannten Projektionsebene. Man erhält
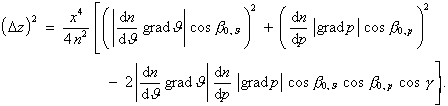 |
(3.3.62) |
Da aber die Richtungen der Temperaturgradienten bei vertretbarem Aufwand nicht oder nur sehr ungenau meßbar sind, wird auf eine exakte, vektorielle Berechnung der Richtung der resultierenden Abweichung verzichtet.
Die Ablenkung des Laserstrahls durch Schallwellen nach Gl. (3.3.56) liegt allgemein in einer dritten, von Druck- und Temperaturgradient unabhängigen Ebene. Die Addition von Gl. (3.3.56) zu der Gradientenablenkung (3.3.62) erfolgt analog zu Gl. (3.3.61). Auf eine Ausführung dieser formalen Operation wird hier ebenfalls verzichtet.
Zur Abschätzung des Maximalfehlers erfolgt eine Addition der Beträge der einzelnen Fehler (Gln. (3.3.30), (3.3.48) und (3.3.56)). Es ergibt sich
| (3.3.63) |
mit
| (3.3.63a) |
für Werkstattbedingungen.
Nach Abhandlung der Arten und Größen der auftretenden Fehler soll es im weiteren darum gehen, die Einflüsse der Fehler auf die einzelnen Messungen zu untersuchen und einen resultierenden Gesamtfehler zu ermitteln.
Erster Untersuchungsgegenstand sind die Einflüsse der oben genannten Fehler auf die Entfernungsmessung. Der größeren Empfindlichkeit wegen beziehen sich die folgenden Betrachtungen ausschließlich auf Planspiegelanordnungen, die dazu analoge Behandlung der Aufbauten mit Tripelreflektoren erfolgt nicht. Deshalb unterbleibt die im Kapitel 2 vorgenommene Unterscheidung der Indizes "P" und "T" an den Meßgrößen.
Die bereits im Kapitel 3.3.1 ermittelten, aus den Brechzahlparameterfehlern resultierenden Meßfehler von
| (3.3.9) | |
| (3.3.13) |
(die x-Achse entspricht der idealen Strahlrichtung des Meßstrahles) stellen eine Hauptfehlerquelle der Entfernungsmessung dar. Der Nullpunkt der x-Koordinate liegt dabei in der planspiegelseitigen Oberfläche der l/4-Platte des Meßarmes der Interferometeranordnung ((e) in Bild 2.2.1), der in (3.3.9) bzw. (3.3.12) eingehende x-Wert wird durch die Planspiegelfläche definiert. Der Fehler Dx ist also unabhängig von der Position der Rücksetzung (Nullung) der Auswerteeinheit und beinhaltet auch den durch den Totweg (Weg x abzüglich des mit dem Meßspiegel seit der Nullung zurückgelegten Meßwegs). Eine Möglichkeit der Reduktion des Totwegs bildet der Einsatz eines Differentialspiegelinterferometers (Bild 2.2.3), der Weg x ist dann die Länge der Meßstrecke, wenn sich der Referenzspiegel bezüglich seiner x-Koordinate innerhalb oder an einem Ende der Meßstrecke befindet.
Eine weitere Hauptfehlerquelle stellt der Einfluß der Umgebungsgeräusche (Schall) dar. Da die Umgebungsgeräusche nicht nur, wie zur Gewinnung der Gl. (3.3.60a) angenommen wurde, aus einer reinen Sinuswelle, sondern aus einem ganzen Spektrum bestehen, kann als Meßfehler nicht die numerisch korrigierbare, sinusförmige Beeinflussung des Meßwertes angenommen werden. Vielmehr muß die gesamte Amplitude als schallverursachter Meßfehler
| (3.3.60b) |
genutzt werden. Bei der statischen Vermessung einzelner Punkte, wie sie z. B. während der Maschinenabnahme nach /3/ erfolgt, ist es möglich, diesen Fehler durch statistische Mittelung zu eliminieren. Nimmt man allerdings den Verlauf einer Bewegung dynamisch (z.B. zeitlich getaktet) auf, dann geht der Fehler (3.3.60b) voll in den Gesamtmeßfehler ein.
Zusätzlich üben die in den Kapiteln 3.3.3 - 3.3.6 ermittelten und in Gl. (3.3.63) zusammengefaßten Geradheitsabweichungen einen Einfluß auf das Meßergebnis aus: Durch die Krümmung kommt es zu einer geringfügigen Verlängerung der Meßstrecke. Diese berechnet sich unabhängig von der Anzahl der optischen Interpolationen zu
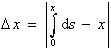 |
(3.3.64) |
Unter Verwendung des Wegelementes
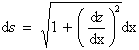 |
(3.3.65) |
ergibt sich
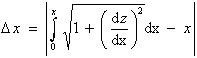 |
(3.3.64a) |
woraus nach Einsetzen der Ableitung der Gl. (3.3.63)
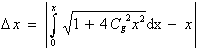 |
(3.3.64b) |
folgt. Ein Einsetzen der Reihenentwicklung der Wurzel um x = 0 ( wegen Cg « 1 möglich ) liefert
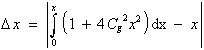 |
(3.3.64c) |
Nach Ausführung der Integration ergibt sich
| (3.3.64d) |
Die sich wegen Cg @ 10-6 ergebende Verfälschung des Meßwertes liegt über Meßentfernungen von x < 20 m um mehrere Größenordnungen unter der der Gln. (3.3.9) bzw. (3.3.12) und ist daher zu vernachlässigen. Der atmosphärische Einfluß auf die Längenmessung reduziert sich damit für alle für die Messungen mit dem ZLM 300 relevanten Entfernungen auf den unmittelbaren Einfluß der Brechzahlunsicherheit nach den Gln. (3.3.9) bzw. (3.3.12).
Die an der Anordnung zur Winkelmessung (Bild 2.2.6) auftretenden statisch-atmosphärischen Meßfehler beschränken sich auf die im Kapitel 3.3.1 ermittelten Abweichungen
| ohne und | (3.3.10) | |
| mit automatischer Umweltkompensation | (3.3.14) |
Der Punkt a = 0 wird dabei durch den physikalischen Nullpunkt (vgl. Kap. 2.2.2) definiert.
Wegen des auf der Differenzentfernungsmessung beruhenden Winkelmeßprinzips kompensieren sich die infolge eines evtl. vorhandenen Druck- oder Temperaturgefälles vorhandenen Abweichungen innerhalb des Meß- und des Referenzarms, sie wirken sich daher nicht auf das Ergebnis aus. Bei auftretenden Schallwellen, die sich im ungünstigsten Fall senkrecht zur Laserstrahlrichtung ausbreiten, ist eine gegensinnige Abweichung der optischen Weglängen von Meß- und Referenzstrahl möglich. Diese erreicht ihr Maximum, wenn die halbe Schallwellenlänge mit dem Abstand des Meß- und Referenzstrahls übereinstimmt. Das ist aber erst bei Frequenzen n » 4 kHz gegeben. Wegen der verschwindend geringen Amplituden dieser Frequenzen und der statistischen Verteilung der Ausbreitungsrichtungen der Umgebungsgeräusche kann dieser Einfluß vernachlässigt werden. Diese Vernachlässigbarkeit gilt selbstverständlich auch für den Differentialanteil bei Längenmessungen mit Differentalinterferometern (Bild 2.2.2 und 2.2.3).
Im Kapitel 3.3.1 ergaben sich die direkt aus der Brechzahlunsicherheit resultierenden Meßfehler zu
| Doppelkeil 1, ohne automat. Umweltkomp. | (3.3.11b) | |
| Doppelkeil 2, ohne automat. Umweltkomp. | (3.3.11c) |
woraus sich für beide Doppelkeile der zu vernachlässigende Fehler
| (3.3.12) |
ergab.
Weiterhin ergaben sich bei vorhandenen Druck- oder Temperaturgradienten Geradheitsabweichungen des Laserstrahls zu
| (3.3.63) |
mit Cg nach Gl. (3.3.63a). Diese beeinflussen unmittelbar die Ergebnisse der einzelnen Meßpunkte zi(xi), haben aber auf die Geradheitsabweichung Dz(x) einen geringeren Einfluß: Durch die als Geradheitsbezug dienende Ausgleichsgerade, die sich aus den Meßwerten zi(xi) berechnet, verringert sich der in das Ergebnis eingehende Fehler entsprechend. Der gegen die durch die nach Gl. (3.3.63) abweichenden Meßpunkte verlaufende Ausgleichsgerade resultierende Fehler soll ermittelt werden. Dazu nutzen wir die Gauß'sche Methode der kleinsten Quadrate, bei der die Konstanten a und b der durch die Meßwerte (xi; Dzi) verlaufenden Ausgleichsgerade Dz = ax + b durch die Forderung der Minimierung der Funktion
| (3.3.66) |
bestimmt sind. In unserem an Stelle der Meßpunkte vorhandenen Kontinuum (3.3.63) nimmt Gl. (3.3.66) die Form
| (3.3.66a) |
an, wobei die Punkte x=0, xe bzw. xa durch den Eintritt des Laserstrahls in die Atmosphäre, das laserabgewandte bzw. laserseitige Ende der Meßstrecke bestimmt sind. F(x,a,b) ergibt sich zu
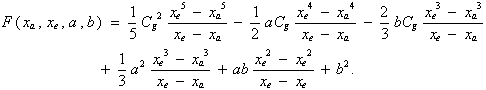 |
(3.3.67) |
Zur Ermittlung der Minima in a und b setze man die partiellen Ableitungen gleich Null
| (3.3.68) |
| (3.3.69) |
und löse das durch die Gln. (3.3.68) und (3.3.69) gebildete Gleichungssystem. Als Lösung ergibt sich
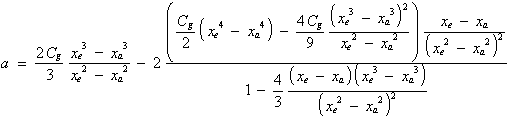 |
(3.3.70) |
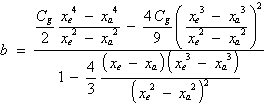 |
(3.3.71) |
Für xa = 0 wird wegen der Maximierung der Meßstrecke der Fehler maximal, a und b gehen über in
| (3.3.70a) | |
| (3.3.71a) |
In diesem Fall ergibt sich der Fehler zu
| (3.3.72) |
mit Cg nach Gl. (3.3.63a). Eine graphische Darstellung zeigt Bild 3.3.13.
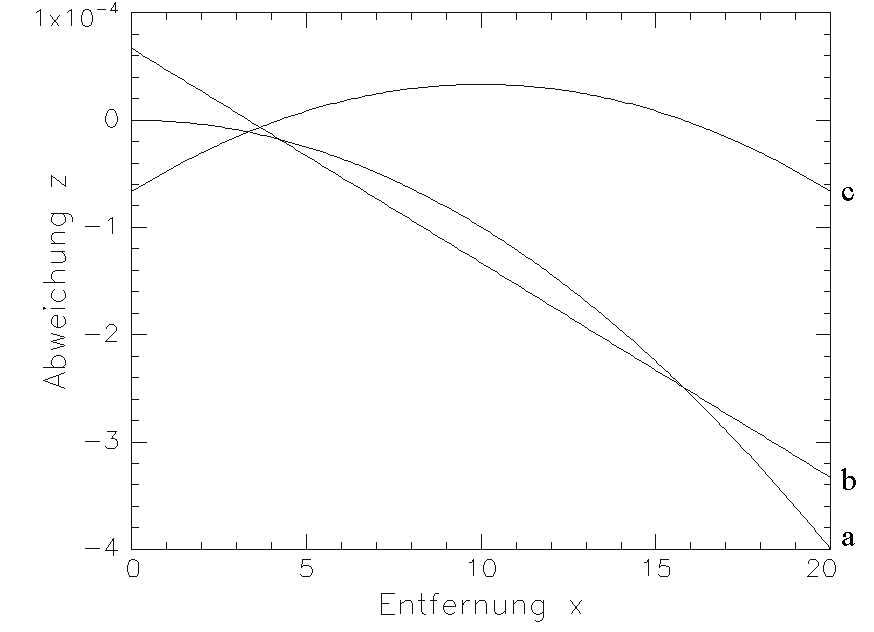
Nach dieser Beschreibung der statisch-atmosphärischen Meßfehler sollen nun die statistischen Einflüsse der Atmosphäre untersucht werden.
Das Problem der Ausbreitung der Laserstrahlung durch die Atmosphäre ist bereits in vielen Arbeiten einer Untersuchung zugeführt worden. Beispiele dafür sind /41/, /44/, /47/, /48/, /49/, /50/, /51/, /52/ und /53/, wobei eine fundierte theoretische Beschreibung in /48/ und eine mehr praktischere Beschreibung in /44/ enthalten ist. Nach diesen Arbeiten lassen sich die statistischen Einflüsse anhand von räumlichen und zeitlichen Korrelationsfunktionen der Brechzahldifferenz behandeln, die bei verschwindenden Korrelationsparametern in die quadratisch räumlich bzw. zeitlich gemittelten Brechzahlschwankungen übergehen. Diese Brechzahlschwankungen verursachen Intensitäts- und Phasenschwankungen, Strahlverbreiterungen, Strahlrichtungsänderungen und damit natürlich Schwankungen der Meßwerte. Nach Messungen von Buck /52/ erhöht sich beispielsweise der Strahldurchmesser bei wachsender Entfernung x > 100 m zusätzlich um einen Faktor 5Öx zur natürlichen Divergenz des Gauß'schen Bündeldurchmessers am Ort x, was aber bei für das ZLM 300 üblichen Meßentfernungen keine Rolle spielt. Ebenso vernachlässigbar sind Intensitätsfluktuationen, wie in /51/, /52/ und /53/ beschrieben, da das im ZLM 300 genutzte Verfahren auf der Zählung der Differenzfrequenz der beiden Lasermoden (vgl. Kap. 2) beruht. Es bleiben die direkten Einflüsse der statistischen Brechzahlschwankungen und die Strahlrichtungsänderungen bzw. Strahllageabweichungen, die nachfolgend einer Betrachtung zugeführt werden sollen.
Um die statistische Einwirkung der Brechzahl auf die Strahlausbreitung beurteilen zu können, ist es sinnvoll, sich mit der Natur der Turbulenzen zu befassen, da ihre Einflüsse die der reinen Fluktuationen der Brechzahlparameter Druck und Temperatur weit überschreiten.
Schwankungen des Brechungsindex, meist verursacht durch Temperaturfluktuationen, aber auch durch Druckfluktuationen und durch Luftbewegungen (Wind), sind Zufallsfunktionen in Raum und Zeit. Sie werden durch räumliche und zeitliche Korrelationsfunktionen beschrieben, die unter der Annahme der Homogenität und Isotropie nur vom Abstand der Raum- bzw. Zeitpunkte abhängen:
| (3..4.1) | |
|
(3.4.2) |
Nach /47/, /44/ gilt für die räumliche Abhängigkeit für das sogenannte "Zwei-Drittel-Gesetz", das für kleine Abstände r durch ein quadratisches Gesetz ersetzt wird
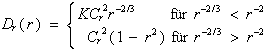 |
(3.4.3) |
wobei Cr die räumlich quadratisch gemittelte Brechzahlschwankung des Turbulenzelements und K eine Konstante bezeichnet. In ein bis zwei Meter Höhe über der Erdoberfläche liegt sie in der Größenordnung /44/
| (3.4.4) |
Wegen der Ergodizität des Systems stimmt diese mit der zeitlichen quadratisch gemittelten Brechzahlschwankung überein. Ebenso ist daher ein zeitliches "Zwei-Drittel-Gesetz" zu fordern.
Zur Abschätzung des Einflusses der Turbulenzen stellt man sich die Atmosphäre als eine Ansammlung von Turbulenzelementen vor /41/. Die mittlere Größe des Turbulenzelements Lr definiert sich dann als die Entfernung, nach welcher die Korrelationsfunktion auf einen vordefinierten Teil ihres Maximums abgefallen ist. Sie liegt im Bereich
| Lr = 1 mm ... 3 m. | (3.4.5) |
Das Resultat der Ausbreitung der Laserstrahlung ist von der Größe der Turbulenzelemente abhängig (Bild 3.4.1) und umfaßt Brechungen, Streuungen und Fokussierungen/Defokussierungen, die wegen des statistischen Charakters der Turbulenzen alle gleichzeitig auftreten. Eine Reflexion an den Turbulenzelementen kann wegen des in praxi kontinuierlichen Brechzahlverlaufs und der sehr geringen Schwankungen ausgeschlossen werden.
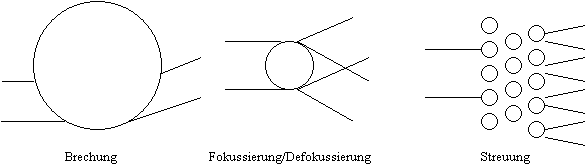
Bild 3.4.1: Wirkung der Turbulenzelemente auf das sich ausbreitende Laserbündel
Zur Abschätzung der einzelnen Einflüsse sollen im folgenden die "reinen" Effekte der Darstellungen des Bildes 3.4.1 betrachtet werden.
Für Turbulenzelemente der Größe Lr << d (d...Strahldurchmesser) überwiegt die streuende Wirkung, deren Stärke die der Streuung der ruhenden Atmosphäre übersteigt /44/. Diese Streuung verursacht einen Abfall der an der Empfangsdiode einfallenden Leistung, die aber wegen der hohen Leistungsreserven des ZLM 300 vernachlässigt werden kann.
Ist die Größe der Turbulenzelemente dagegen groß gegen den Querschnitt des sich ausbreitenden Bündels ( Lr >> d ), dann tritt die brechende Wirkung in den Vordergrund. Ihr Einfluß soll nachfolgend ermittelt werden. Dazu betrachten wir die Ausbreitung in positiver x-Richtung der Strahlung durch ein Turbulenzelement der Länge Lx und der Breite Lz zum festen, beliebigen Zeitpunkt t0 (Bild 3.4.2). Wegen der geringen Brechzahldifferenz Dn ist die Verwendung des differentiellen Brechungsgesetzes
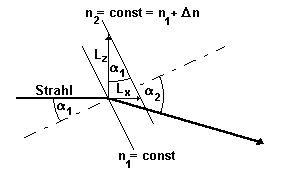
Bild 3.4.2: Ablenkung eines Strahles an einem Turbulenzelement
| (3.3.24a) |
möglich. Der Tangens des Einfallswinkels berechnet sich nach Bild 2.4.2 zu
| (3.4.6) |
Unter Berücksichtigung der Isotropie der Turbulenzen ergibt sich das quadratische Mittel über alle Turbulenzelemente
| (3.4.7) |
Dies entspricht einem Einfallswinkel von a = 45&#deg;. Die mittlere Ablenkung pro Turbulenzelement in der x-z-Ebene beträgt daher
| (3.4.8) |
Dieses Ergebnis stimmt mit denen von Schüßler /41/ und Hodara /44/ überein. Zur Ermittlung der mittleren Gesamtablenkung über die Wegstrecke x (o.B.d.A. x0=0) argumentiert Hodara mit der statistischen Unabhängigkeit der Turbulenzelemente und addiert deshalb über die Anzahl der Turbulenzelemente
| (3.4.9) |
Diese Abschätzung ist aber relativ grob, da sie die Gleichwahrscheinlichkeit der positiven und negativen Vorzeichen der Ablenkung am einzelnen Turbulenzelement nicht genügend respektiert. Schüßler führt einen von der Anzahl der Turbulenzelemente abhängigen Korrekturfaktor ein, den er nicht näher spezifiziert.
Als Lösung des Problems eignet sich ein "Random-Walk"-Prozeß, der sich durch eine Binomialverteilung beschreiben läßt. Das Ereignis der Wahrscheinlichkeit p bildet die Ablenkung am Turbulenzelement mit Da > 0, das Nichtereignis der Wahrscheinlichkeit q = p - 1 bildet die Ablenkung am Turbulenzelement mit Da < 0, wobei p = q = 0,5 gilt. Die Wahrscheinlichkeit des k-maligen Eintrittes des Ereignisses bei Ablenkung an A Turbulenzelementen ist dann
| (3.4.10) |
Nach dem Lokalen Grenzwertsatz von Moivre-Laplace /43/ konvergiert für eine sehr große Anzahl von Turbulenzelementen die Binomialverteilung gegen die Normalverteilung. Die Standardabweichung der Normalverteilung berechnet sich dabei nach
| (3.4.11) |
Den resultierenden, quadratisch gemittelten Gesamtablenkwinkel erhält man mit
| (3.4.12) | |
| (3.4.12a) |
woraus die quadratisch gemittelte Gesamtablenkung nach
| (3.4.13) | |
| (3.4.13a) | |
| (3.4.13b) | |
| (3.4.13c) |
folgt.
Eine analoge Betrachtung der x-y-Ebene muß infolge der Isotropie auf das äquivalente Ergebnis führen. Für den Betrag der Winkelabweichung gegen die x-Achse ergibt sich
| (3.4.14) | |
| (3.4.15) |
die Richtungen der Abweichungen (Azimute) sind isotrop und damit gleichverteilt. Eine Darstellung der Gleichung (3.4.15) zeigt Bild 3.4.3.
Als dritter zu behandelnder Fall soll abschließend die fokussierende/defokussierende Wirkung behandelt werden. Sie tritt auf, wenn die Größe der Turbulenzelemente in der Größenordnung des Strahldurchmessers liegt. Die einzelnen Turbulenzelemente wirken dann wie Stanhopesche Linsen, deren Brennweite abhängig vom Linsenradius r
| (3.4.16) |
beträgt /54/. Für den Randstrahl des aus dem Unendlichen auf die Linse einfallenden Bündels ergibt sich dann die Ablenkung (Bild 3.4.4) am Turbulenzelement
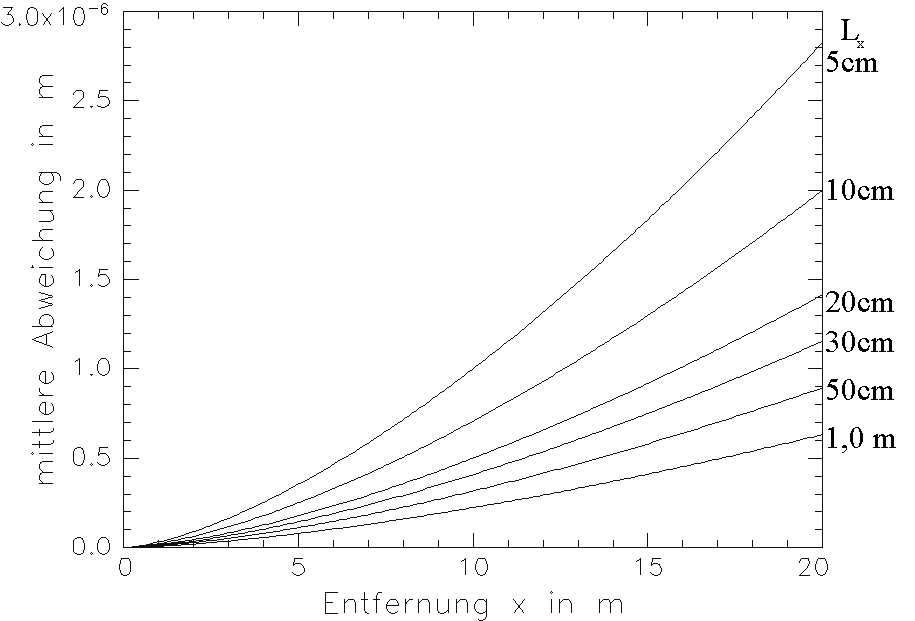
Bild 3.4.3: Quadratisch gemittelte Abweichung des Laserstrahls von seiner mittleren Lage in Abhängigkeit von der Entfernung vom Laser für verschieden große Turbulenzelemente des Durchmessers Lx und eine quadratisch gemittelte Brechzahl von 10-8
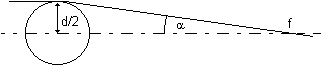
Bild 3.4.4: Ablenkung eines Strahles an einem Turbulenzelement
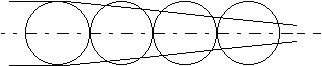
Bild 3.4.5: Ablenkung des Randstrahles eines Bündels an einer Kette von Turbulenzelementen
| (3.4.17) |
Da die Ablenkung wegen n << 1 sehr gering ist, kann man (3.4.17) näherungsweise auf alle Turbulenzelemente einer "Turbulenzelementekette" (Bild 3.4.5) verallgemeinern /41/. Die Abweichung pro Länge ergibt sich dann nach
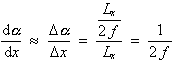 |
(3.4.18) |
Durch Integration mit a0 = 0 folgt
| (3.4.19) |
Die Abweichung senkrecht zur Ausbreitungsrichtung ist nach der einfachen Dreiecksbeziehung
| (3.4.20) |
woraus unter Nutzung der Gln. (3.4.16) und (3.4.19)
| (3.4.20a) |
folgt. Unter Beachtung erstens des statistischen Charakters der Brechzahl und zweitens der Eindeutigkeit der optischen Abbildung ergibt sich die quadratisch gemittelte Änderung des Strahldurchmessers
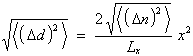 |
(3.4.20b) |
was sowohl Fokussierung (Bild 3.4.5) als auch Defokussierung (Bild 3.4.6) bedeuten kann.
Bild 3.4.6: Defokussierung des Laserbündels
Die hier angeführte Abschätzung ist zwar wegen der Annahme der "Turbulenzelementekette" recht grob, kann aber als Maximalabschätzung gelten, da sich in beiden Fällen (Bilder 3.4.5/6) die Abweichungen aller Elemente vorzeichenrichtig addieren. Eine graphische Darstellung der Gleichung (3.4.20) zeigt Bild 3.4.7.
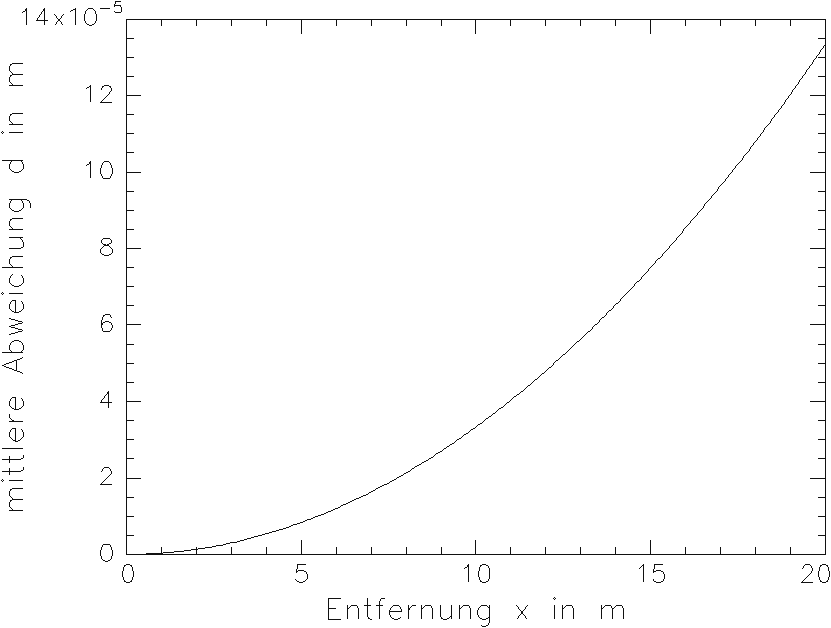
Bild 3.4.7: Quadratisch gemittelte Abweichung des Laserbündeldurchmessers von seinem Mittelwert in Abhängigkeit von der zurückgelegten Entfernung für eine quadratisch gemittelte Brechzahldifferenz von 10-8 und eine Größe der Turbulenzelemente von Lx = 6 mm
Daß Abweichungen dieser Größe in praktischen Experimenten nicht beobachtet wurden, kann nur in der Größe und statistischen Verteilung der Turbulenzelemente begründet liegen, deren Untersuchung allerdings nicht Gegenstand dieser Arbeit ist.
Um die Auswirkungen der Brechzahlschwankungen auf die Längenmessung beurteilen zu können, gehe man den einfachsten Weg und setze ihre mittlere Schwankung in Gleichung (3.3.6) ein. Es ergibt sich
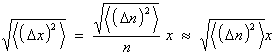 |
(3.4.21) |
Wie aber spätere Betrachtungen zeigen werden, ist die Allgemeingültigkeit der Gl. (3.4.21) nicht gegeben. Da sie die statistische Unabhängigkeit der Brechzahlschwankungen längs des Weges nicht berücksichtigt, gilt sie nur über die Länge des jeweiligen Turbulenzelementes.
Darüber hinaus folgt aus der seitlichen Abweichung des Strahles von seiner Mittellage ein Längenfehler, der sich analog zur Gleichung (3.3.65) herleiten läßt und unter Nutzung von Gleichung (3.4.15) den Wert
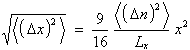 |
(3.4.22) |
besitzt. Er ist jedoch vernachlässigbar, da er á(Dn)2ñ beträgt. Entscheidet man sich bei der Messungen von Entfernungen (z.B. bei der Maschinenabnahme) für Schrittverfahren /3/, bei denen die einzelnen Entfernungen des Bewegungsablaufes in ruhender Position des Meßspiegels genommen werden, so ist es möglich, an jedem Meßpunkt mehrere Meßwerte in die Auswerteeinheit einzulesen und diese jeweils statistisch zu mitteln. In diesem Fall muß Gleichung (3.4.21) nicht im Meßfehler berücksichtigt werden. Führt man jedoch die Messungen dynamisch, d. h. während der Bewegung des Meßspiegels durch, so ist diese Mittelung nicht möglich; die Meßwerte erhalten einen zusätzlichen mittleren Meßfehler entsprechend Gl. (3.4.21).
Das im vorangegangenen Kapitel zur Längenmessung Gesagte gilt sinngemäß für jeden der beiden Meßarme der Winkel- und Geradheitsmessung. Nimmt man die statistische Unabhängigkeit der Turbulenzen in den Meßarmen voneinander an, ergibt sich die quadratisch gemittelte Entfernungsdifferenz der Meßarme durch m-malige quadratische Addition der Gleichung (3.4.21) mit sich selbst. m ist dabei die Anzahl der nicht ineinander verlaufenden und nicht durch Tripelprismenversatz (für die Bilder 2.2.5 und 2.2.6 gilt m = 2) erzeugten Meß- und Referenzstrahlenpaare zwischen Strahlteiler und Reflektor. Diese Abgrenzung ist sicher etwas willkürlich, jedoch ist der Abstand der Meß- und Referenzstrahlenpaare mit r = 4 cm doppelt so groß, wie der 2-cm-Abstand des Tripelprismenversatzes. Das Ergebnis muß nun noch durch m geteilt werden, um die entsprechend höhere optische Interpolation bei Vorhandensein mehrerer Strahlen m zu berücksichtigen. Es ergibt sich
| (3.4.23) |
Unter Zuhilfenahme der Dreiecksrelation (2.2.3) folgt für die Winkelmeßinterferometer nach Bild 2.2.5 und Bild 2.2.6
| (3.4.24) |
Beachtung verdient hier die Tatsache, daß x / r nicht den Kippwinkel a, sondern daß x » xmeß » xref die Entfernung vom Polarisationsstrahlteiler zum Spiegel (Bild 2.2.6) bezeichnet. Dennoch sind Zweifel an der Gültigkeit der Gln. (3.4.23/24) berechtigt, da die Frage der statistischen Unabhängigkeit der Fluktuationen in den einzelnen Teilstrahlen nicht exakt beantwortet werden kann. Bei Turbulenzen, deren Größe den Abstand der Strahlen des Meß- und Referenzarms überschreitet, ist davon auszugehen, daß sich die Abweichungen teilweise kompensieren. Gleichung (3.4.24) besitzt daher den Charakter einer "statistischen Maximalabschätzung". Das im vorherigen Kapitel bezüglich der Schritt- bzw. dynamischen Messungen Gesagte gilt bei der Winkelmessung sinngemäß.
Eine ähnliche Überlegung ließe sich noch für Gl. (3.4.22) durchführen, sie kann aber aus dem dort bereits erwähnten Grund unterbleiben.
Die Abweichungen der Gl. (3.4.23) wirken sich mittels Gl. (2.2.17) auf die Ergebnisse der Geradheitsmessungen aus. Man erhält für den statistischen Geradheitsfehler
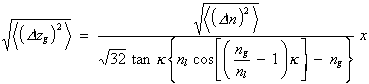 |
(3.4.25) |
Zusätzlich dazu wirken sich natürlich die Geradheitsschwankungen des Laserstrahls unmittelbar auf das Meßergebnis aus. Dazu ist Gleichung (3.4.13c) zu nutzen (nicht Gleichung (3.4.15)), da die Geradheitsmessungen immer nur in einer Ebene stattfinden. Um beide Fehler zusammenzuführen, ist es notwendig, den statistischen Charakter zu beachten. Die Fehler nach Gl. (3.4.25) hängen statistisch nur vom Betrag der mittleren Brechzahlschwankungen des Turbulenzelements ab, die Geradheitsfehler des Strahles selbst aber wesentlich von der Lage der Turbulenzelemente (Bild 3.4.5). Daher kann von einer statistischen Unabhängigkeit der Gln. (3.4.25) und (3.4.13c) ausgegangen werden. Der Gesamtmeßfehler ergibt sich durch quadratische Addition unter der Wurzel zu
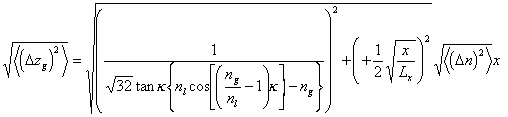 |
(3.4.26) |
Die Darstellung dieser Gleichung für Doppelkeil 1 zeigt Bild 3.4.8.
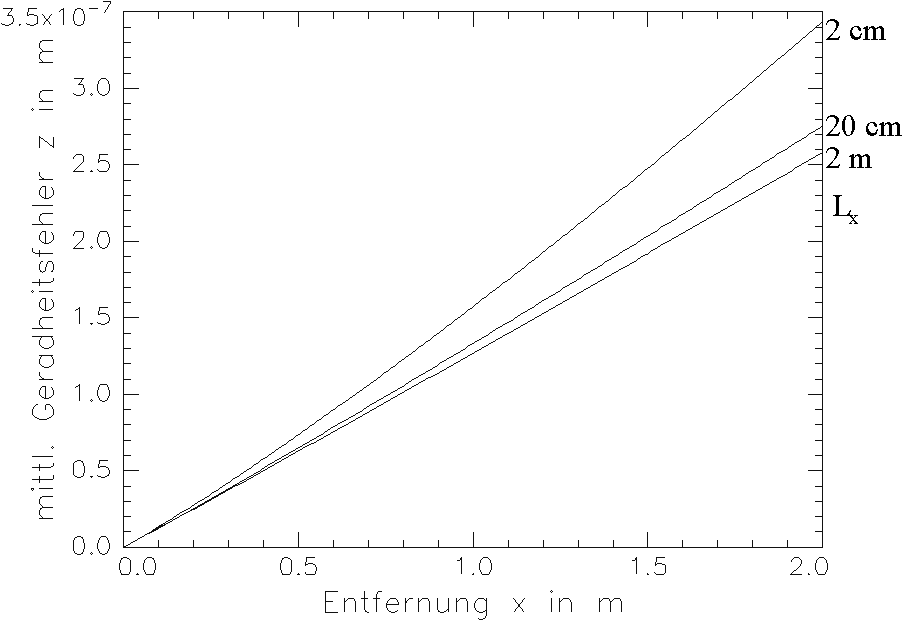
Bild 3.4.8: quadratisch gemittelte Geradheitsabweichung in Abhängigkeit der Entfernung Strahlteiler-Spiegel bei einer mittleren Brechzahlschwankung Öá(Dn)2ñ = 10-8 und verschieden großen Turbulenzelementen
Die Messungen mit dem Laserwegmeßsystem ZLM 300 beruhen auf der durch die Dopplerfrequenz im Meßarm des Interferometers (vgl. Kap. 2.1) erzeugten Abweichung des Heterodynsignals vom ungestörten Heterodynsignal des Referenzkanales.
Bewegt man (Bild 2.2.2 oder 2.2.3) nun gleichzeitig zum Meßreflektor den Referenzreflektor, so treten diese Dopplerverschiebungen in beiden Interferometerarmen auf und kompensieren daher in erster Näherung einander. Da sich aber bei heterodyn arbeitenden Systemen Licht unterschiedlicher Frequenz im Meß- bzw. Referenzarm befindet, kompensieren sich die Dopplerverschiebungen nicht vollständig. Es verbleibt eine Differenz, die nachfolgend am Beispiel der Meßanordnung des Bildes 2.2.2 berechnet werden soll.
Bei der Bewegung der Meßreflektors mit der Geschwindigkeit vm entsteht die Dopplerfrequenzverschiebung
| (2.1.1) |
bei der Bewegung der Geschwindigkeit vr des Referenzreflektors die Dopplerfrequenzverschiebung
| (3.5.1) |
Die daraus resultierende Abweichung der Dopplerverschiebung der Heterodynfrequenz
| (3.5.2) |
setzen wir in Gl. (2.1.8) ein und erhalten
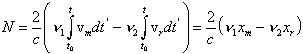 |
(3.5.3) |
Ersetzt man den Weg des Meßreflektors xm durch die Summe des Weges des Referenzspiegels xr und die Differenz xD des Meßspiegelwegs zum Referenzspiegelweg
| (3.5.4) |
dann ergibt sich aus Gl. (3.5.3)
| (3.5.5) |
Unter Einsetzen von Gl. (2.1.10) folgt
| (3.5.6) |
Um den vom Meßsystem angezeigten Wert zu erhalten, muß Gl. (3.5.6) in Gl. (2.1.8c) eingesetzt werden, die in der Auswerteeinheit für die Ermittlung des Weges aus den vom Zähler bereitgestellten Werten verantwortlich ist. Man erhält den Meßwert des Systems zu
| (3.5.7) |
bzw.
| (3.5.7a) |
In Spezialfall xr = 0 verschwindet der zweite Term in Gl. (3.5.7a), der Meßwert entspricht dem zurückgelegten Weg xD = x. Durch jede Bewegung des Referenzreflektors entsteht jedoch der Fehler
| (3.5.8) |
Da in Gl. (3.5.8) kein Faktor für verschiedene optische Interpolationen der Meßanordnung vorhanden ist, gilt sie für Anordnungen nach Bild 2.2.3 gleichermaßen.
Für die Winkelmessung nach Bild 2.2.5 oder 2.2.6 mit während der Messung längs der Strahlrichtung um den Weg x verschobenem Reflektor erhält man den Heterodynfehler Da durch Einsetzen der Gl. (3.5.8) in Gl. (2.2.3), woraus bei einem Abstand der Meß- und Referenzstrahlen von r = 40 mm
| (3.5.9) |
folgt. Bei Messungen mit in x-Richtung festem Reflektor entsteht der von der Lage der Kippachse des Reflektors abhängige Fehler
| (3.5.9a) |
der verschwindet, wenn sich der Stahl der Frequenz n1 mit der Kippachse schneidet, und der seinen Maximalwert annimmt, wenn sich der Stahl der Frequenz n2 mit der Kippachse schneidet.
Geradheitsmessungen (Bild 2.2.7) erfolgen immer derart, daß der Winkelspiegel fest steht und das Doppelkeilprisma bewegt wird. Ein aus der Bewegung des Winkelspiegels resultierender Fehler entsteht nicht. Bewegt man jedoch das Doppelkeilprisma in der für die Geradheitsmessung empfindlichen Richtung, so entsteht nach Gl. (2.2.17) eine optische Weglängendifferenz. Da diese gleichermaßen auf der vorzeichengegensätzlichen Veränderung der optischen Weglängen im Meß- und im Referenzstrahl um jeweils den halben Betrag beruht, kann man sich - gedanklich verglichen mit der Anordnung nach Bild 2.2.3 - die gleiche Weglängendifferenz durch Verschiebung der Reflektoren um jeweils Dx/2 nach Gl. (2.2.17) erzeugt vorstellen. Daher ist jeder Geradheitsmeßwert zg mit einem Fehler
| (3.5.10) |
behaftet. Die maximal meßbare Geradheitsabweichung beträgt konstruktiv bedingt ±2mm, woraus der Heterodynfehler der Geradheitsmessung zu
| (3.5.11) |
resultiert. Er kann wegen seiner Kleinheit zu den Geradheitsinkrementen vernachlässigt werden.
Im folgenden Kapitel soll es nun darum gehen, einige der theoretisch behandelten Fehler experimentell zu untersuchen. Dazu wollen wir uns einführend der Längenmessung zuwenden.
Ein wesentlicher Einflußfaktor ist der mit Hilfe der Gln. (3.3.9) und (3.3.12) beschriebene, aus den Parametern der Edléngleichung resultierende Fehler. Dieser konnte nicht untersucht werden, da ein dazu erforderliches Refraktometer (vgl. Kap. 3.3.1) nicht zur Verfügung stand. Weiterhin würde eine exakte Messung dieses Sachverhaltes erfordern, die Meß- und die Refraktometerstrecke örtlich und zeitlich identisch anzuordnen, was unter vertretbarem ökonomischen Aufwand nicht möglich ist. Daher wollen wir uns im folgenden Kapitel der Untersuchung des Einflusses des Schalls nach Kap. 3.3.4.2 zuwenden.
Zur Untersuchung des schallbedingten Längenmeßfehlers wurde ein Versuchsaufbau nach Bild 4.1.1 gewählt.
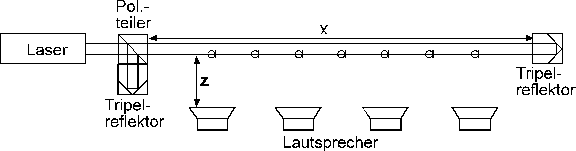
Bild 4.1.1: Anordnung zur Messung des Einflusses des Schalles; es bezeichnen x die Länge der Meßstrecke, z den zum aus dem Laser austretenden Strahl senkrechten Abstand der Lautsprecher und die Mikrofonsymbole die Orte der Schalldruckmessungen
Durch die Anordnung der Lautsprecher sollte unter Ausnutzung des Huygensschen Prinzips eine näherungsweise ebene Schallwelle erzeugt werden. Die Ansteuerung erfolgte über einen Sinusgenerator mit nachgeschaltetem Verstärker, so daß ein Schwingen der Lautsprecher in gleicher Phase gewährleistet war.
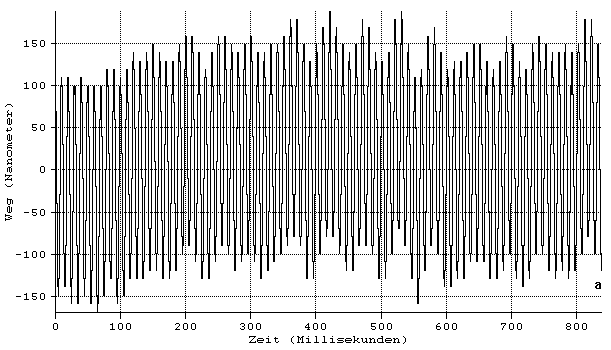
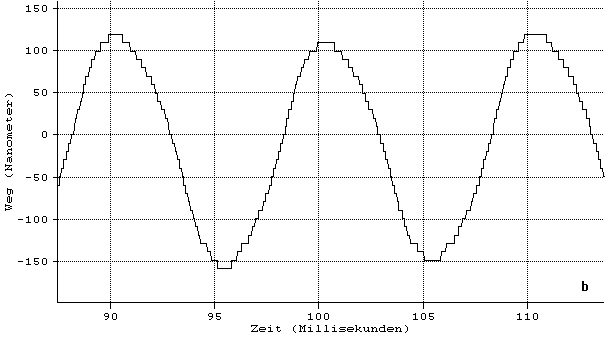
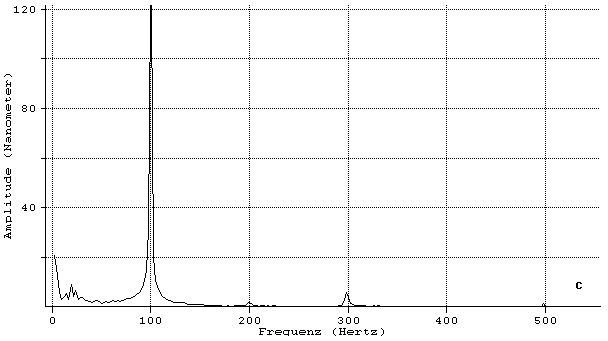
Bild 4.1.2: graphische Darstellung des gesamten Datensatzes (a), eines Teilausschnittes (b) und der Fouriertransformierten (c) der Frequenz ns = 100 Hz und des Schallpegels ps = 103 dB
Der erzeugte Schalldruck wurde unmittelbar über den Lautsprechern und über deren Zwischenräumen am Ort des aus dem Laser austretenden Strahles gemessen. Die Meßwerte des Schalldruckes ps schwankten dabei mit Dps = ± 2 dB um die in Tabelle 4.1.3 angegebenen Werte, wobei die Meßunsicherheit des genutzten Schalldruckmeßgeräts "RFT - integrierender Schallpegelmesser 00026" bei Dps = ± 0,2 dB lag. Die Messungen erfolgten unter Verwendung der linearen Druckbewertungskurve (alle Frequenzen gleichberechtigt) über eine Integrationszeit von jeweils zwei Sekunden. Zur Ermittlung des Länge der Meßstrecke x = 1,50 m (Bild 4.1.1) und des Abstandes z = 0,30 m diente ein Stahlbandmaß mit einer teilungsbedingten Meßunsicherheit von Dx = Dz = ± 0,01 m. Die Messungen der Amplitude der schalldruckbedingten Schwankungen Dx des Entfernungsmeßwerts erfolgten mit 39062,5 Meßwerten pro Sekunde bei einer Anzahl von 32768 Meßwerten. Das entspricht etwa 390 Meßwerten pro Periode bei 100 Hz. Als Beispiel ist ein solcher Datensatz in Bild 4.1.2 dargestellt.
Aus den so gewonnenen Datenfiles wurden mit Hilfe des Computerprogramms "lärmstat" alle Differenzen der jeweils hintereinander folgenden lokalen Maxima und Minima des betreffenden Datenfiles gemittelt. Die daraus folgenden mittleren Amplituden und ihre empirischen Standardabweichungen sind in Tabelle 4.1.3 angegeben.
| Frequenzns in Hz | Schallpegel ps in dB | mittlere Amplitude Dx in nm | Empir. Standartabweichg. der Amplitude D(Dx) in nm |
| 100 | 84 | 12,9 | 3,8 |
| 100 | 86 | 16,3 | 5,3 |
| 100 | 88 | 23,8 | 5,3 |
| 100 | 92 | 35,3 | 8,8 |
| 100 | 97 | 63,6 | 7,1 |
| 100 | 99 | 89,7 | 13 |
| 100 | 103 | 123 | 17 |
| 200 | 106 | 20,4 | 3,8 |
| 200 | 111 | 42,8 | 4,9 |
| 300 | 104 | 29,9 | 3,2 |
| 300 | 114 | 77,6 | 12 |
Wie die Werte in Tabelle 4.1.3 zeigen, verändern sich die Amplituden der Schwingungen des Entfernungsmeßwerts mit der Frequenz. Das ist darauf zurückzuführen, daß die erzeugten Schallwellen nicht eben waren. Legt man die Anordnung nach Abbildung 4.1.1 zugrunde, so hätte zur Herleitung der Amplitude (3.3.60b) anstelle der Druckdifferenz (3.3.57) die Superposition von Kugelwellen
| (4.1.1) |
angesetzt werden müssen. ps,l bezeichnet dabei den Schallpegel unmittelbar am Ort der Lautsprechermembranen. Berücksichtigt wurde in Gl. (4.1.1) weiterhin der von Gl. (3.3.51) abweichende Bezugspegel
| (4.1.1a) |
des o.g. Schalldruckmeßgeräts. Diesen Spezialfall wollen wir aber nicht weiter verfolgen, vielmehr soll es um eine Abschätzung der Gültigkeit der Amplitude (3.3.60b) gehen, die unter Berücksichtigung von Gl. (4.1.1a) den Wert
| (3.3.60c) |
annimmt. Dazu wurde mit den Werten ps = 100 dB eine logarithmische Regression /55/ (Bild 4.1.4, links) durchgeführt, in deren Ergebnis sich der Zusammenhang
| (4.1.2) |
beziehungsweise der im Bild 4.1.4 (rechts) dargestellte äquivalente Zusammenhang
| (4.1.2a) |
ergab. Eine Betrachtung von Gl. (4.1.2a) zeigt, daß der im Exponenten stehende Faktor mit dem aus der Theorie ermittelten in Gl. (3.3.60c) innerhalb der Fehlergrenzen übereinstimmt, was als eine Bestätigung der Gl. (3.3.60c) gewertet werden kann. Die Abweichung des Vorfaktors der Gln. (3.3.60c) und (4.1.2a) ist auf die teilweise Unebenheit der verursachenden Schallwelle zurückzuführen. In jedem Falle behält Gl. (3.3.60c) bzw. die sich auf die internationale Definition des Bezugsschalldrucks beziehende Gl. (3.3.60b) als maximal mögliche Amplitude Bestand, da die durch sie vorgegebene Amplitude nicht überschritten wurde.
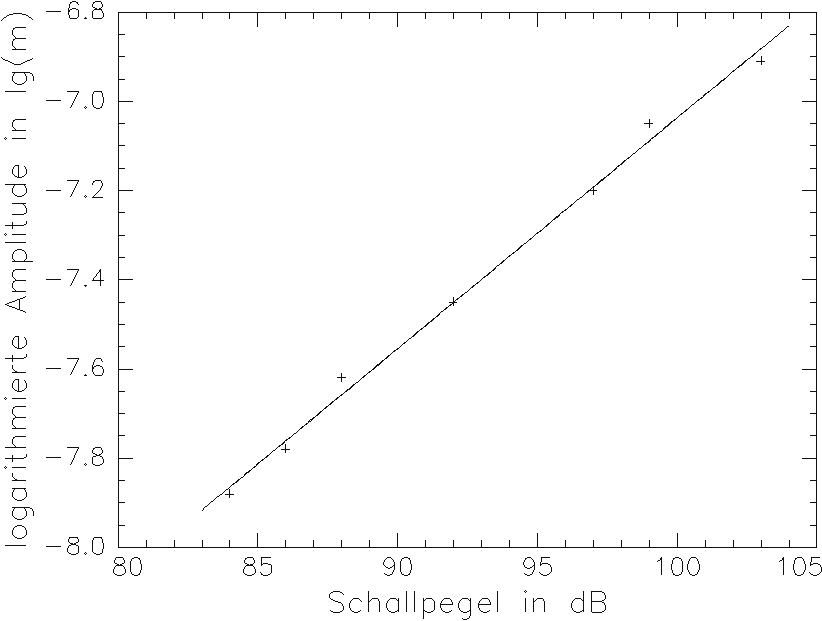
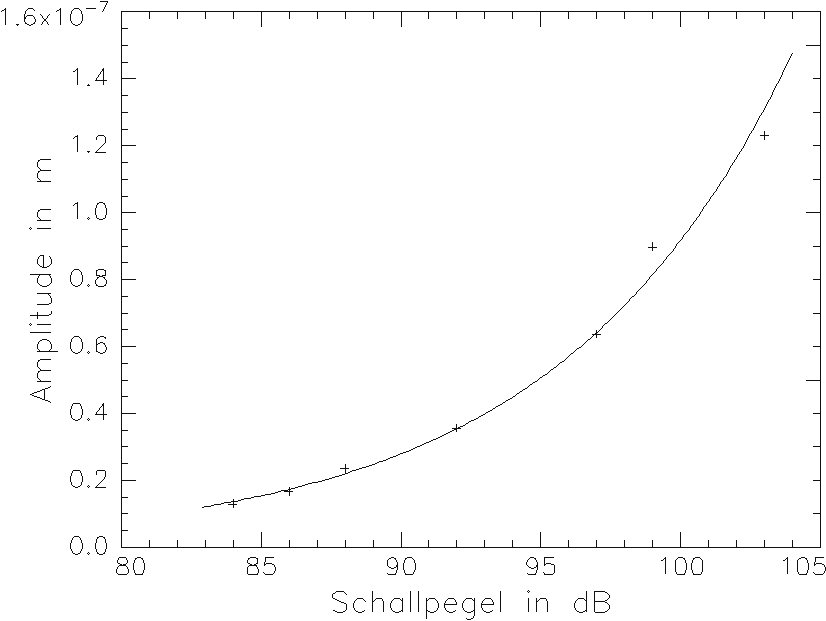
Bild 4.1.4: Darstellung der mittleren Amplituden (oben) und ihrer Logarithmen (unten) der 100 Hz - Meßwerte über den verursachenden Schallpegeln
Abschließend soll noch eine kurze Anmerkung zur Wahl der Frequenz erfolgen: Die Ebenheit der Schallwellen würde sich für ls ® ¥ bzw. ns ® 0 verbessern. Dies zu realisieren war technisch leider nicht möglich, da sich für ns < 100 Hz die Übertragungs- und Verstärkungseigenschaften des zur Ansteuerung der Lautsprecher verwandten Verstärkers rapide verschlechterten. Daher stellte die Verwendung der Frequenz ns = 100 Hz das technisch realisierbare Optimum dar. Die Aufnahme der Werte für die beiden Frequenzen ns = 200 Hz und ns = 300 Hz dienen nur zu einer qualitativen Bestätigung der Abhängigkeit der Amplitude des Entfernungsmeßfehlers von der Frequenz bei Verwendung nichtebener Wellen.
Die Untersuchung der statistischen Längenmeßfehler bildet eine wesentliche Grundlage des zur Längen- und Winkelmessungen zu wählenden Meßregimes, da auf deren Grundlage die Auswahl der Meß- bzw. Mittelungszeiten erfolgen muß. Dabei kann eine Unterscheidung nach Meßanordnungen mit Planspiegeln oder Tripelprismen entfallen, da die sich mehrfach selbst überdeckenden Strahlen der Planspiegelanordnungen nur einen um den optischen Interpolationsfaktor erhöhten Brechzahleinfluß zur Folge haben, durch den bei der Gewinnung der Meßwerte im PC wieder dividiert wird. Das Meßergebnis verändert sich dadurch letztlich nicht, es wird nur eine an dieser Stelle nicht erforderliche Verbesserung der Auflösung (Inkrement) erreicht. Hingegen sind die einfachen Längenmeßanordnungen (Bilder 2.1.1 und 2.2.1) von denen der Differential- und Winkelmeßanordnungen (Bilder 2.2.2, 2.2.3, 2.2.5 und 2.2.6) zu unterscheiden, weil bei letzteren Anordnungen die im Kap. 3.4 behandelten statistischen Fehler auf Meß- und Referenzstrahlen wirken und sich dadurch teilweise gegenseitig kompensieren. Daher wollen wir uns nachfolgend zuerst der Untersuchung der einfachen Meßanordnungen zuwenden.
Grundlage der Untersuchungen bildet die Meßanordnung nach Bild 2.1.1. Diese wurde für unterschiedliche, während der einzelnen Messungen unterschiedlicher Meßzeiten konstant gehaltene Entfernungen aufgebaut. Die Meßstrahlen verliefen dabei in einem Abstand von ca. 120 cm parallel zum Fußboden. Innerhalb der einzelnen Meßentfernungen erfolgte die Aufnahme je eines Datensatzes von 32768 Meßpunkten für unterschiedliche Meßzeiten. Alle Datensätze wurden bei abgeschalteter Klimaanlage aufgenommen, da die systematischen, jedoch in ihrer Vielfalt nicht erfaßbaren Einflüsse der Klimaanlage die eigentlichen statistischen Fehlereinflüsse deutlich übertrafen (Bild 4.1.5).
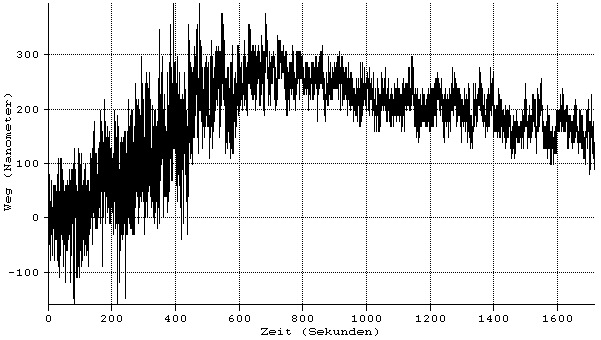
Bild 4.1.5: Einfluß der Klimaanlage auf die Schwankungen des Entfernungsmeßwerts bei einer Meßentfernung von x = 2m; etwa 600 Sekunden nach Beginn der Messungen wurde die Klimaanlage abgeschaltet
Die so gewonnenen Meßwertfiles wurden mit Hilfe des Programms "zlm-stat" (Anlage 2) einer Gaußstatistik unterworfen. Die daraus gewonnenen empirischen Standardabweichungen (Tabelle 4.1.6) sollten ein Maß für die statistischen Brechzahlschwankungen sein, da wegen Gl.
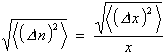 |
(4.1.3) |
gilt. Die Werte der quadratisch gemittelten Brechzahlen nach Gl. (4.1.3) zeigt Tabelle 4.1.7, eine Darstellung ihrer raümlichen und zeitlichen Mittelwerte Bild 4.1.8.
| x in m | ||||||||||
| t in s | 1,00 | 2,00 | 3,00 | 4,00 | 5,00 | 6,00 | 7,00 | 8,00 | 9,00 | 10,00 |
| 0,4 | 8,6 | 11,8 | 10,8 | 11,6 | 9,9 | 31,5 | 12,7 | 15,4 | 14,1 | 22,1 |
| 0,8 | 13,1 | 15,6 | 13,4 | 10,4 | 13,1 | 25,7 | 12,4 | 15,0 | 17,7 | 21,6 |
| 1,6 | 11,1 | 13,2 | 12,1 | 11,2 | 10,4 | 12,0 | 19,5 | 22,0 | 18,3 | 23,1 |
| 3,3 | 12,0 | 17,3 | 9,5 | 13,0 | 20,9 | 29,1 | 27,0 | 27,2 | 27,8 | 34,4 |
| 6,7 | 15,4 | 15,6 | 16,7 | 11,8 | 13,9 | 34,0 | 32,9 | 33,6 | 31,4 | 46,1 |
| 13,4 | 15,8 | 19,1 | 18,4 | 16,6 | 27,0 | 37,2 | 28,7 | 40,5 | 52,0 | 26,6 |
| 26,8 | 29,4 | 27,1 | 16,2 | 35,2 | 38,9 | 47,3 | 65,1 | 43,2 | 30,0 | 63,3 |
| 53,6 | 22,0 | 29,6 | 94,0 | 63,5 | 49,2 | 50,7 | 82,1 | 72,0 | 82,1 | 75,7 |
| 107,4 | 44,2 | 28,2 | 31,5 | 72,0 | 64,4 | 74,0 | 63,7 | 74,0 | 105,0 | 93,6 |
| 215,2 | 55,6 | 88,4 | 74,5 | 165,0 | 120,0 | 83,3 | 114,0 | 92,7 | 117,0 | 128,0 |
| 429,5 | 76,4 | 370,0 | 377,0 | 359,0 | 349,0 | 117,0 | 121,0 | 195,0 | 120,0 | 123,0 |
| x in m | |||||||||||
| t in s | 1,00 | 2,00 | 3,00 | 4,00 | 5,00 | 6,00 | 7,00 | 8,00 | 9,00 | 10,00 | Mittel |
| 0,42 | 8,64 | 5,90 | 3,60 | 2,90 | 1,99 | 5,25 | 1,81 | 1,93 | 1,57 | 2,21 | 3,58 |
| 0,83 | 13,10 | 7,80 | 4,47 | 2,60 | 2,62 | 4,28 | 1,77 | 1,88 | 1,97 | 2,16 | 4,26 |
| 1,68 | 11,10 | 6,60 | 4,03 | 2,80 | 2,08 | 2,00 | 2,79 | 2,75 | 2,03 | 2,31 | 3,85 |
| 3,36 | 12,00 | 8,65 | 3,18 | 3,25 | 4,18 | 4,85 | 3,86 | 3,40 | 3,09 | 3,44 | 4,99 |
| 6,71 | 15,40 | 7,80 | 5,57 | 2,95 | 2,78 | 5,67 | 4,70 | 4,20 | 3,49 | 4,61 | 5,72 |
| 13,43 | 15,80 | 9,55 | 6,13 | 4,15 | 5,40 | 6,20 | 4,10 | 5,06 | 5,78 | 2,66 | 6,48 |
| 26,84 | 29,40 | 13,55 | 5,40 | 8,80 | 7,78 | 7,88 | 9,30 | 5,40 | 3,33 | 6,33 | 9,72 |
| 53,69 | 22,00 | 14,80 | 31,33 | 15,88 | 9,84 | 8,45 | 11,73 | 9,00 | 9,12 | 7,57 | 13,97 |
| 107,40 | 44,20 | 14,10 | 10,50 | 18,00 | 12,88 | 12,33 | 9,10 | 9,25 | 11,67 | 9,36 | 15,14 |
| 215,20 | 55,60 | 44,20 | 24,83 | 41,25 | 24,00 | 13,88 | 16,29 | 11,59 | 13,00 | 12,80 | 25,74 |
| 429,50 | 76,40 | 185,00 | 125,67 | 89,75 | 69,80 | 19,50 | 17,29 | 24,38 | 13,33 | 12,30 | 63,34 |
| Mittel | 27,60 | 28,90 | 20,43 | 17,48 | 13,03 | 8,21 | 7,52 | 7,17 | 6,22 | 5,98 | |

Bild 4.1.8: Darstellung der in Tabelle 4.1.7 berechneten zeitlichen (oben) bzw. räumlichen (unten) Mittelwerte über der Meßentfernung (links) bzw. über der Meßzeit (rechts)
Entgegen der nach Gl. (4.1.3) erwarteten Unabhängigkeit der empirischen Standartabweichung der Brechzahl von Meßzeit und Meßentfernung zeigt sich, daß dieser mit der Zeit zu- und mit der Meßentfernung sogar abnimmt. Infolge dessen muß, wie bereis in Kap. 3.4 erwähnt, die Allgemeingültigkeit der aus Gl. (3.3.6) folgenden Gl. (3.4.21) angezweifelt werden. Streng hat Gl. (3.4.21) wegen der Beschränkung der Gl. (3.4.4) auf ein Turbulenzelement ebenfalls nur diesen Geltungsbereich und kann offensichtlich nicht auf die gesamte Meßentfernung ausgedehnt werden. Die Zweifel erhärten sich weiterhin dadurch, daß Gl. (3.4.21) nicht die statistische Unabhängigkeit der einzelnen Wegelemente der Meßstrecke berücksichtigt. Folglich wäre die Gültigkeit von Gl. (4.1.3) ebenfalls nicht mehr gegeben.
Deshalb soll ein neuer, von der Theorie der Turbulenzelemente unabhängiger und auf der Homogenität des Raumes beruhender Ansatz verfolgt werden, der einerseits die statistische Unabhängigkeit der einzelnen Meßstreckenelemente berücksichtigt, und der andererseits die Ergodizität von Zeit und Raum enthält. Die diesen Ansatz folgende Hypothese der Existenz einer weg- und zeitunabhängigen Streukonstante S
| (4.1.4) |
wollen wir nachfolgend näher untersuchen. Dazu wurden die empirischen Standardabweichungen mit der Meßentfernung x (Bild 4.1.9, links) bzw. der Zeit t (Bild 4.1.9, rechts) normiert und über die einzelnen Meßzeiten t bzw. Meßentfernungen x gemittelt. Teilt man diese Mittelwerte durch die Wurzel der Meßzeit t bzw. der Meßentfernung x, dann erhält man die durch Gl. (4.1.4) definierte Konstante S der jeweiligen Meßreihe.
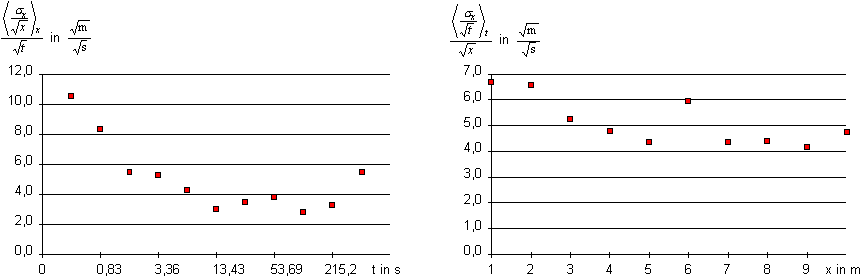
Bild 4.1.9: Darstellung der Streukonstante S für die einzelnen, innerhalb der Meßzeit (links) bzw. der Meßentfernung (rechts) gemittelten Meßreihen
Eine Betrachtung der einzelnen Meßreihenkonstanten S macht uns dabei auf mögliche Meßfehler einer Reihe aufmerksam. So weicht die Streukonstante der Messungen mit der Meßzeiten t = 0,41 s (Bild 4.1.9, links) von den anderen Streukonstanten ab. Die Ursache dessen ist in der Kürze der Meßzeit zu suchen, in der, bedingt durch die Diskretheit des Inkrements (2.1.12) des Meßsystems, keine Normalverteilung gegeben ist. Die Messung dieser Meßzeit wird daher aus der Berechnung der Streukonstanten ausgeschlossen. Betrachten wir nun die rechte Darstellung der Bildes 4.1.9. In dieser Darstellung zeigen die Werte geringer Meßentfernungen eine Abweichung vom Mittelwert. Das ist wahrscheinlich darauf zurückzuführen, daß der Experimentator, genötigt durch die räumlichen Gegebenheiten des Meßlabors, in nur einem Meter Abstand zum Polarisationsstrahlteiler der Anordnung nach Bild 2.1.1 saß. Dadurch sind Beeinflussungen der Brechzahl möglich, die mit zunehmender Entfernung (größer werdender Meßstrecke) abnehmen. Da diese Beeinflussungen nicht gravierend sind, wird auf einen Ausschluß dieser Meßwerte verzichtet.
Unter Beachtung der Aussagen des vorhergehenden Ansatzes ergibt sich die Streukonstante S nach
| (4.1.5) |
zu
| (4.1.6) |
wobei die Indizes n und m die einzelnen Messungen nach Weg und Zeit bezeichnen. Da die Reihenfolge der Summation vertauschbar ist, bleibt es mathematisch gesehen gleich, diese aus den unter Ausschluß obengenannter Messungen neu ermittelten Werten der rechten oder der linken Darstellung des Bildes 4.1.9 zu mitteln. Die in Gl. (4.1.6) angegebene Fehlergrenze entspricht der empirischen Standardabweichung der gemittelten Werte.
Um die Einflüsse der Turbulenzelemente abschätzen zu können, erfolgte analog zur Gewinnung der bisherigen Meßwerte dieses Kapitels die Aufnahme neuer Meßwerte. Dabei verliefen die Meßstrahlen in einem Abstand von ca. 10 cm parallel zum Fußboden, was die Bildung größerer Turbulenzelemente verhindern sollte. Es ergaben sich die in Tabelle (4.1.10) angegebenen Werte, die ebenfalls die empirischen Standartabweichungen über 32768 Meßwerte des jeweiligen Datensatzes sind.
| x in m | ||||||||||
| t in s | 1,00 | 2,00 | 3,00 | 4,00 | 5,00 | 6,00 | 7,00 | 8,00 | 9,00 | 10,00 |
| 0,8 | 4,7 | 4,2 | 3,3 | 4,6 | 6,3 | 5,4 | 7,4 | 5,1 | 6,8 | 12,7 |
| 1,7 | 9,7 | 7,1 | 6,9 | 17,2 | 18,8 | 11,2 | 10,2 | 18,4 | 12,6 | 29,9 |
| 3,4 | 18,7 | 7,6 | 18,1 | 13,9 | 10,5 | 14,3 | 14,3 | 34,4 | 48,9 | 16,6 |
| 6,7 | 11,9 | 16,5 | 24,2 | 12,5 | 39,3 | 29,4 | 46,0 | 30,3 | 53,5 | 42,9 |
| 13,4 | 13,9 | 34,0 | 37,2 | 55,5 | 60,9 | 34,8 | 35,0 | 28,9 | 93,5 | 79,5 |
| 26,8 | 18,0 | 38,2 | 53,6 | 42,4 | 51,9 | 48,3 | 56,9 | 55,0 | 58,2 | 132,0 |
| 53,7 | 20,8 | 38,3 | 55,3 | 46,9 | 58,5 | 66,2 | 94,1 | 108,0 | 99,9 | 120,0 |
| 107,4 | 31,6 | 55,2 | 51,2 | 56,3 | 76,2 | 73,6 | 83,9 | 112,0 | 140,0 | 131,0 |
| 215,2 | 42,0 | 40,1 | 60,1 | 51,6 | 92,1 | 179,0 | 98,1 | 145,0 | 125,0 | 218,0 |
| 429,5 | 38,3 | 41,2 | 77,4 | 78,3 | 99,7 | 144,0 | 125,0 | 161,0 | 170,0 | 187,0 |
Ebenfalls analog zur Berechnung der Punkte des Bild 4.1.9 wurden die Werte der Darstellungen des Bildes 4.1.11 gewonnen, wobei auf Grund der Erkenntnisse von oben keine Messungen mit der Meßzeit t = 0,42 s durchgeführt wurden. Diese Messungen erhärten mit ihren Werten die Gültigkeit der Hypothese 4.1.4.
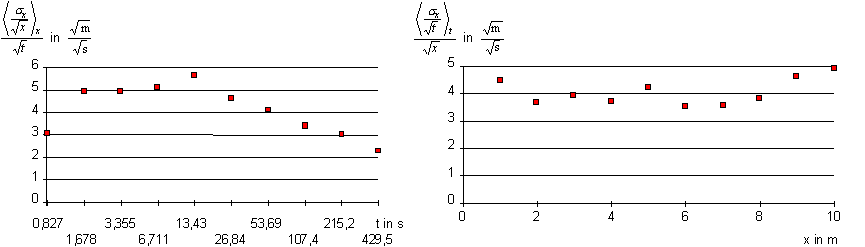
Bild 4.1.11: Darstellung der Streukonstante S für die einzelnen, innerhalb der Meßzeit (links) bzw. der Meßentfernung (rechts) gemittelten Meßreihen der Meßwerte in Bodennähe
Dabei fällt auf, daß die Schwankungen der einzelnen Werte beider Darstellungen des Bildes 4.1.11 unter denen des Bildes 4.1.9 liegen. Offensichtlich ist, durch die Bodennähe bedingt, die Schwankungsbreite der Streukonstante geringer. Die Berechnung der Streukonstante S nach Gl. (4.1.5) ergibt
| (4.1.7) |
Danach ist der Mittelwert der Streukonstante annähernd konstant, lediglich ihre Schwankungsbreite ist geringer. Letztlich wären zu einer exakteren Untersuchung und Bestimmung der Streukonstante weitere, vielfältige Messungen erforderlich. Solche umfangreichen Untersuchungen würden aber den Rahmen dieser Diplomarbeit sprengen. Darüber ist die Möglichkeit ihrer Realisierung durch materielle Zwänge innerhalb der Carl Zeiss Jena GmbH beschränkt.
Die im Kapitel 4.1.2.1 durchgeführten Messungen sollen nun unter Verwendung eines Differentialtripelinterferometeraufbaus (Bild 2.2.2) wiederholt werden. Dabei waren beide Tripelreflektoren fest miteinander verbunden, Meß- und Referenzstrecke hatten die gleiche Länge und den (parallelen) Abstand von 4 cm. Die nachfolgenden Tabellenwerte stellen wiederum eine Mittelung über die jeweils 32768 Meßpunkte eines Datensatzes dar. Es ergaben sich bei den Messungen in einer Höhe von 120 cm über dem Boden die in Tabelle (4.1.12) angegebenen Werte. Die Messungen in 10 cm Höhe wurden unter Berücksichtigung der noch darzustellenden Ergebnisse der Meßwerte in Tabelle 4.1.12 bei verlängerten Meßzeiten gewonnen. Sie erbrachten die empirischen Standardabweichungen der Tabelle (4.1.13).
| x in m | ||||||||||
| t in s | 1,00 | 2,00 | 3,00 | 4,00 | 5,00 | 6,00 | 7,00 | 8,00 | 9,00 | 10,00 |
| 26,8 | 6,6 | 7,4 | 5,2 | 9,7 | 13,4 | 13,8 | 17,3 | 20,3 | 14,3 | 15,6 |
| 53,7 | 8,7 | 13,2 | 5,1 | 10,6 | 16,5 | 18,5 | 18,7 | 24,4 | 17,2 | 18,4 |
| 107,4 | 10,2 | 9,1 | 9,3 | 11,3 | 15,7 | 21,9 | 17,7 | 28,3 | 20,4 | 23,5 |
| 215,2 | 11,7 | 6,6 | 11,1 | 12,9 | 18,6 | 23,6 | 19,7 | 27,6 | 26,0 | 20,3 |
| 429,5 | 16,8 | 13,9 | 19,2 | 17,4 | 19,7 | - | 23,7 | 33,2 | 35,4 | 36,6 |
| x in m | ||||||||||
| t in s | 1,00 | 2,00 | 3,00 | 4,00 | 5,00 | 6,00 | 7,00 | 8,00 | 9,00 | 10,00 |
| 53,7 | - | 30,2 | - | 34,5 | 37,4 | 41,0 | 49,0 | 57,5 | 63,7 | 50,2 |
| 107,4 | 17,9 | 22,3 | 20,2 | 26,3 | 29,0 | 48,4 | 46,4 | 34,9 | 72,5 | 40,3 |
| 215,2 | 18,7 | 21,1 | 29,9 | 32,3 | 34,2 | 33,2 | 46,5 | 52,5 | 48,5 | 46,0 |
| 429,5 | 20,6 | 23,9 | 21,6 | 34,8 | 35,2 | 35,2 | 43,2 | 52,5 | 63,4 | 45,0 |
| 858,9 | 20,5 | 26,8 | 24,7 | 42,2 | 36,4 | 43,2 | 48,0 | 60,9 | 61,3 | 60,9 |
Analog zur Berechnung der Punkte des Bild 4.1.9 wurden die Werte der Darstellungen des Bildes 4.1.14 bzw. 4.1.15 für die Meßhöhen 120 cm bzw. 10 cm gewonnen.
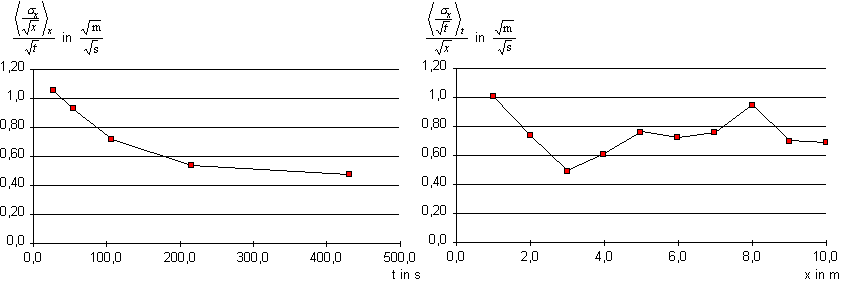
Bild 4.1.14: Darstellung der Streukonstante S für die einzelnen, innerhalb der Meßzeit (links) bzw. der Meßentfernung (rechts) gemittelten Meßreihen der Meßwerte der Tabelle (4.1.12)
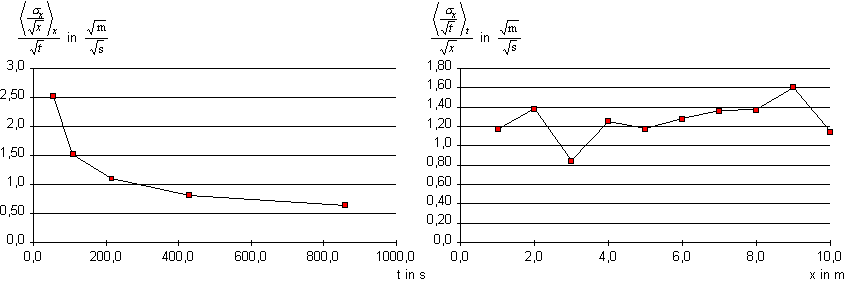
Bild 4.1.15: Darstellung der Streukonstante S für die einzelnen, innerhalb der Meßzeit (links) bzw. der Meßentfernung (rechts) gemittelten Meßreihen der Meßwerte der Tabelle (4.1.13)
Die rechten Darstellungen der Bilder (4.1.14) und (4.1.15) zeigen die innerhalb einer Schwankungsbreite erwartete Gleichheit der Streukonstante entsprechend der in Gl. (4.1.4) formulierten Hypothese. Vergleicht man aber die Darstellungen genauer, dann fällt auf, daß (entgegen den Ergebnissen des vorangegangenen Kapitels) die Streukonstante in Bodennähe einen höheren Wert besitzt als die in 120 cm Höhe gemessene. Die Erklärung hierfür liegt nach unserer Ansicht in der Tatsache begründet, daß bei den Messungen in Bodennähe die "Randbereiche" der Turbulenzelemente stärker zur Wirkung kommen, hingegen können bei den bodenfernen Messungen nahezu alle Bereiche der Turbulenzelemente gleichmäßig einwirken. Dadurch wird letztlich die zeitliche statistische Gleichverteilung der turbulenten Zustände über den gesamten Meßraum gestört.
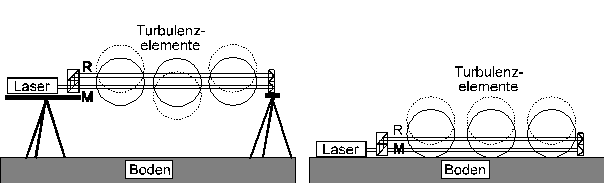
Bild 4.1.16: Darstellung der unterschiedlichen Wirkmöglichkeiten der Turbulenzelemente (stark vergrößert) in Bodenferne (links) und in Bodennähe (rechts); M und R bezeichnen den Meß- und den Referenzarm des Interferometers
Eine Illustration dieses Sachverhaltes zeigt Bild 4.1.16. Bewegen sich nun beide Turbulenzelemente des Bildes 4.1.16 gleichmäßig um den Betrag des Abstandes der Meß- und Referenzstrahlen von der Erdoberfläche weg, so ist die in der rechten Anordnung erzielte Differenz der optischen Weglängen des Meß- und Referenzstrahls größer, als die in der linken Anordnung erzielte. Da nun der links illustrierte Fall in Bodennähe nicht vorkommen kann, muß die Streukonstante in der rechten Anordnung des Bildes 4.1.16 etwas größer sein als die Streukonstante bei Nutzung der linken Anordnung.
Beim Vergleich der linken Diagramme der Bilder 4.1.14 und 4.1.15 zeigt sich eine Abnahme der Streukonstante bei zunehmenden Meßzeiten. Ursächlich dafür könnte die geringe Bewegungsgeschwindigkeit der Turbulenzelemente sein, in deren Folge die zeitliche statistische Gleichverteilung der turbulenten Zustände über den gesamten Meßraum erst über größere Meßzeiträume gesichert ist. Zur Bestätigung der Richtigkeit dieser Annahme müßten weitere Messungen über längere Zeiträume erfolgen. Die daraus resultierenden Werte der Streukonstante sollten sich dann einem Grenzwert annähern, der der Streukonstante bei völliger zeitlicher Gleichverteilung entspricht. Da eine nähere Untersuchung dieses Sachverhaltes hohe materielle Aufwendungen (Verhinderung von Driften der Brechzahl, separater Meßraum in einen möglichst gut von der Umwelt entkoppelten Gebäude) erfordert, konnte diese Annahme nicht weiter verfolgt werden.
Die aus der statistischen Behandlung aller in der jeweiligen Tabelle dargestellten Werte nach Gl. (4.1.5) resultierenden Streukonstanten in 120 cm Höhe
| (4.1.8) |
und in 20 cm Höhe
| (4.1.9) |
über dem Boden dürften wegen der im Vorabsatz angeführten Argumentation gegenüber den bei völliger Gleichverteilung gültigen Werten etwas zu hoch sein.
Die Einflüsse der einwirkenden Umwelt entsprechen wegen der prinzipiellen Gleichheit der Meßanordnungen nach Bild 2.2.2 und Bild 2.2.5 bzw. nach Bild 2.2.4 und Bild 2.2.6 denen der Differentialanordnungen. Daher lassen sich die Überlegungen des Kapitels 4.1.2.2 übertragen. Dabei muß beachtet werden, daß sich die alle Ergebnisse nach Gl. (2.2.3) umrechnen. Daher ergeben sich die für die Winkelmessung geltenden Streukonstanten zu
| (4.2.1) |
für 120 cm Höhe und zu
| (4.2.2) |
für 20 cm Höhe über und parallel zu dem Fußboden. Die empirischen Standardabweichungen der Messungen selbst errechnen sich in Anlehnung an Gl. (4.1.5) nach
| (4.2.3) |
worin x der zur Messung verwandte Abstand der Strahlteilers zum Meßspiegel bzw. zu den Tripelprismen ist.
Der Einfluß der Schallwellen konnte nicht nachgewiesen werden, er ist daher, wie bereits in Kapitel 3.3.7 ausgeführt, vernachlässigbar.
Nachdem wir uns bisher mit der Untersuchung der Längen- und Winkelmeßfehler befaßten, wollen wir uns nun wieder dem hauptsächlichen Thema dieser Arbeit zuwenden: den Untersuchungen der Umwelteinflüsse auf die Geradheitsmessungen. Dazu soll zu Beginn der bereits in Kap. 3.3.3 beschriebene Einfluß eines Temperaturgradienten auf die Ausbreitungsrichtung des Laserstrahls beschrieben werden.
Ein Problem hinsichtlich der Messungen stellte die Erzeugung eines definierten Temperaturgradienten dar. Da die Anordnung punktueller und ausreichend starker Wärmequellen unausweichlich die Ausbildung von nicht definierten Turbulenzen und Strömungen zur Folge gehabt hätte, schied die Erzeugung eines annähernd homogenen Temperaturgradienten auf diese Weise aus. Die Anordnung eines Rasters von Konstantandrähten und deren Erwärmung vermittels des elektrischen Stromes schied ebenfalls aus, weil die dadurch erzeugte Wärmeenergie nicht ausreichend war. Der unter den gegebenen Umständen einzig mögliche Weg war die Verwendung der im Raum entstehenden natürlichen Temperaturschichtung. Dazu wurde ein Versuchsaufbau gewählt (Bild 4.3.1), der die Messung der Geradheitsabweichung und gleichzeitig der Temperaturverteilung in einer senkrecht zum Fußboden stehenden, den Laserstrahl enthaltenden Ebene gestattet.
Zur Temperaturmessung fand das Präzisionstemperaturmeßgerät TEMP 10 der Carl Zeiss Jena GmbH Verwendung, wobei die zur Messung genutzten Sensoren nach Auskunft des Entwicklers des Gerätes, Herrn Dr. Tschach, eine Meßunsicherheit von DJ = ± 10 mK besaßen. Die Temperaturmeßwerte wurden in Abständen von einer Minute automatisch in einen PC eingelesen und als Datenfile gespeichert. Mit Hilfe des zur Weiterverarbeitung geschaffenen Programms "gradtver" erfolgte die Berechnung des vertikalen Temperaturgradienten als Ausgleichsgerade durch die Temperaturwerte der übereinander angeordneten Sensoren der jeweiligen Reihe.
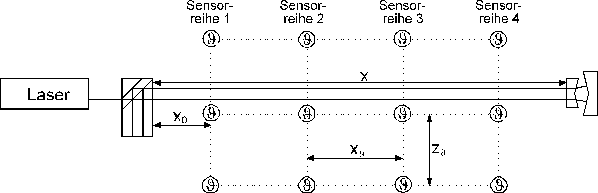
Bild 4.3.1: Anordnung zur Messung der Geradheitsabweichung infolge einer Temperaturschichtung; der optische Aufbau entspricht dem des Bildes 2.2.7, die ![]() - Symbole kennzeichnen die Anordnung der Temperaturfühler, weiterhin bezeichnen x0 = 50 cm den horizontalen Abstand der ersten Sensorreihe zum Strahlteiler, xJ = 100 cm die horizontalen Abstände der Temperatursensoren, zJ = 30 cm die vertikalen Abstände der Temperatursensoren und x = 5 m die Länge der Meßstrecke
- Symbole kennzeichnen die Anordnung der Temperaturfühler, weiterhin bezeichnen x0 = 50 cm den horizontalen Abstand der ersten Sensorreihe zum Strahlteiler, xJ = 100 cm die horizontalen Abstände der Temperatursensoren, zJ = 30 cm die vertikalen Abstände der Temperatursensoren und x = 5 m die Länge der Meßstrecke
Zur Ausbildung der natürlichen Temperaturschichtung wurde die Klimaanlage abgeschaltet und der Raum zwei Stunden nicht betreten. Anschließend erfolgte die Messung der Temperaturverteilung und gleichzeitig (nach Rücksetzung des Nullpunktes) der Geradheit . Der Geradheitsmeßwert beträgt
| (4.3.1) |
und resultiert aus der statistischen Auswertung von 131072 Meßwerten mit Hilfe des Programms "zlm-stat". Die dabei vorhandenen Temperaturgradienten beinhaltet Tabelle 4.3.2.
| Sensorreihe 1 | Sensorreihe 2 | Sensorreihe 3 | Sensorreihe 4 | gesamt | |
| Gradient in &#deg;C/m | 0,39 | 0,47 | 0,30 | 0,30 | 0,36 |
| Fehler d. Grad. in &#deg;C/m | 0,03 | 0,04 | 0,02 | 0,01 | 0,08 |
Nun liefen vier unter der Meßanordnung platzierte Büroventilatoren eine Stunde lang, um die Temperaturschichtung zu zerstören. Die folgende Meßwertnahme ergab wiederum aus 131072 Meßwerten der Geradheitsmeßwert zu
| Sensorreihe 1 | Sensorreihe 2 | Sensorreihe 3 | Sensorreihe 4 | gesamt | |
| Gradient in &#deg;C/m | 0,43 | 0,13 | 0,19 | -0,10 | 0,17 |
| Fehler d. Grad. in &#deg;C/m | 0,05 | 0,06 | 0,04 | 0,03 | 0,20 |
Die aus der Veränderung der Temperaturschichtung resultierende Geradheitsabweichung ergibt sich aus der Differenz der Gln. (4.3.2) und (4.3.1) mit
| (4.3.3) |
Aus Gl. (3.3.30a) ergibt sich unter Einsetzen der Gesamtgradienten der Tabellen 4.2.3 und 4.3.2 anstelle des Terms |gradJ| cosb und Differenzbildung der theoretische Erwartungswert
| (4.3.4) |
Da er ganz erheblich vom Meßwert (4.3.3) abweicht, soll die Berechnung des theoretischen Erwartungswertes auf der Grundlage der Temperaturgradienten der einzelnen Sensorreihen erfolgen. Das trägt weiterhin der starken Abweichung der Gradientenwerte der einzelnen Sensorreihen Rechnung. Dazu wird die Meßentfernung x (Bild 4.3.1) in einen Meter lange Teilstücke unterteilt, deren einzelne Abweichungen unter Berücksichtigung der Abweichungen des einzelnen Meterelementes für die folgenden aufsummiert werden.
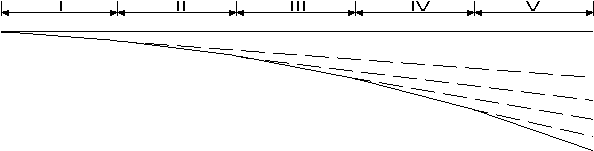
Bild 4.3.4: Ablenkung des Laserstrahls an den einzelnen, mit römischen Zahlen bezeichneten Wegelementen; die durchgezogene, gerade Linie kennzeichnet die Horizontale als Ausbreitungsrichtung des Laserstrahls ohne Temperaturgradient; die durchgezogene, gekrümmte Linie entspricht dem temperaturgradientenbeeinflußten Strahlverlauf und die Strichlinien kennzeichnen die Tangenten an den Strahlverlauf am Ende der Wegelemente
Nach Bild 4.3.4 berechnet sich die Gesamtablenkung aus der Summe der einzelnen Ablenkungen und ihrer tangentialen Fortsetzungen zum Ende der Meßstrecke. Die durch das erste Wegelement der Länge xI am Ende der Meßstrecke hervorgerufene Abweichung DzI berechnet sich aus Dz nach Gl. (3.3.30a) zu
| (4.3.5) |
die des zweiten Wegelementes zu
| (4.3.6) |
usw.. Die Aufsummierung der einzelnen Ablenkungen unter Berücksichtigung der gleichen Länge xi = xI = 1 m aller Teilelemente, der Meßentfernung x = 5 m und der Annahme grad JV = gradJIV ergibt
| (4.3.7) |
Durch Einsetzen der Werte der Tabellen 4.3.2 und 4.3.3 und Differenzbildung der Gl. (4.3.7) erhält man
| (4.3.8) |
Das dieser Wert innerhalb des durch die Meßunsicherheit des Ergebnisses (4.3.3) bestimmten Bereiches liegt, kann er als Bestätigung von Gl. (3.3.30a) interpretiert werden.
Bei weiteren zu dieser Problematik durchgeführten Messungen traten, bedingt durch Fertigungsfehler der optischen Bauteile, große Meßfehler des Laserwegmeßsystems durch unkontrollierte Sprünge des Inkrement-Zählers auf. Deshalb wurde auf eine quantitative Auswertung dieser weiteren Messungen verzichtet. Es ergab sich aber ebenfalls eine qualitative Bestätigung der Gl. (3.3.30a).
Damit sollen die Messungen der temperaturverursachten Fehler beendet werden. Ferner wollen wir uns nun der Untersuchung der Einflüsse eines Druckgradienten auf die Ausbreitung des Laserstrahls zuwenden.
Zur Untersuchung dieser Einflüsse findet ein Versuchsaufbau nach Bild 4.3.5 Verwendung, dessen optischer Aufbau mit dem des Bildes 2.2.7 identisch ist.

Bild 4.3.5: Anordnung zur Messung des Einflusses einer periodisch veränderlichen Druckschichtung; es bezeichnen x = 400 cm die Länge der Meßstrecke, z = 30 cm den zum aus dem Laser austretenden Strahl senkrechten Abstand der Lautsprecher und die Mikrofonsymbole die Orte der Schallpegelmessungen.
Dabei betrug der Abstand des ersten Lautsprechers zum Strahlteiler Dx = 30 cm, die Abstände der Lautsprecher zueinander Dx = 60 cm. Die Erzeugung und Messung der Schalldruckpegel und die Messung aller Entfernungen erfolgte wie in Kap. 4.1.1 beschrieben. Die im Ergebnis der Messung mit Hilfe des Programms "lärmstat" gewonnenen mittleren Amplituden der Geradheitsabweichungen und deren empirische Standardabweichungen zeigt Tabelle 4.3.6.
| Nr. d. Messung | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Frequenz in Hz | 100 | 100 | 200 | 200 | 200 | 300 | 300 | 300 |
| Schallpegel in dB | 100 | 105 | 108 | 108 | 111 | 107 | 108 | 110 |
| mittl. Amplitude in mm | 0,57 | 0,56 | 0,24 | 0,25 | 0,46 | 0,26 | 0,52 | 0,57 |
| St.abw. d. Ampl. in mm | 0,10 | 0,18 | 0,06 | 0,06 | 0,12 | 0,07 | 0,11 | 0,11 |
| theoretischer Ampl. in mm | 0,08 | 0,14 | 0,39 | 0,39 | 0,55 | 0,52 | 0,59 | 0,74 |
Fehler d. th. Ampl. in mm |
0,02 | 0,03 | 0,11 | 0,11 | 0,16 | 0,15 | 0,16 | 0,20 |
Tabelle 4.3.6: mittlere Amplituden und deren empirische Standartabweichungen der Messungen zur schallverursachten Geradheitsabweichung bei gegebener Frequenz und gemessenem Schallpegel sowie der nach Gl. (3.3.56) unter Berücksichtigung von Gl. (4.1.1a) aus Frequenz und Schallpegel berechnete theoretische Wert der Amplitude und dessen aus dem Meßfehler des Schallpegels von Dps = ± 2 dB resultierender Fehler; jeder Amplitudenmeßwert repräsentiert 32768 Meßwerte, gemessen mit 39062,9 Werten pro Sekunde
Innerhalb der Ausnutzung der Fehlergrenzen stimmen die Amplitudenwerte der dritten bis achten Messung überein. Daraus kann die Bestätigung der Gültigkeit der Gl. (3.3.56) aber nur sehr grob abgeleitet werden, da die Ergebnisse der ersten und zweiten Messungen erheblich von den Erwartungen abweichen. Ursache dafür kann die Wechselwirkung der Schallwellen mit den optischen Bauelementen oder dem Laser sein. Die mögliche Ausbildung stehender oder annähernd stehender Wellen im Meßraum scheidet dagegen als Ursache aus, da diese in die Schalldruckmessung eingehen würden.
Messungen bei Frequenzen oberhalb 300 Hz zeigten starke Modulationen (Bild 4.3.7) mit anderen als den jeweiligen Meßfrequenzen, so daß sie für eine experimentelle Überprüfung von Gl. (3.3.56) ausschieden.
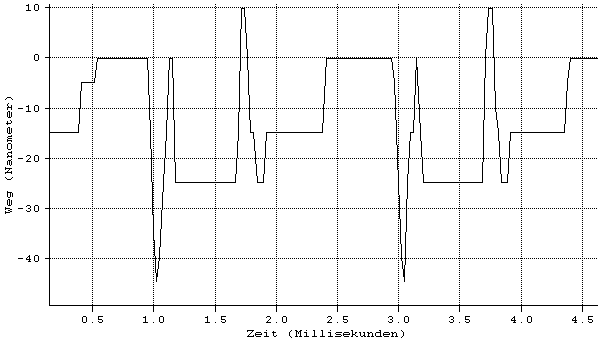
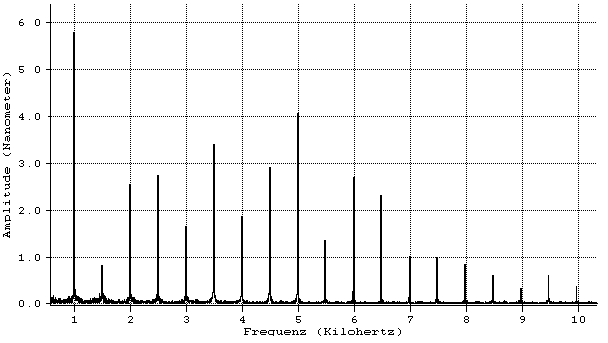
Bild 4.3.7a: Darstellung des Zeitsignals (oben) und der Fouriertransformierten (unten), verursacht durch Modulationen (Fehler) im Verstärker; die eingangsseitig am Verstärker anliegende Frequenz betrug 500 Hz, der erzeugte Schallpegel 106 dB
Abschließend gilt auch hier der Wunsch, zur Untersuchung des Sachverhaltes einen verbesserten Versuchsaufbau verwenden zu können. Eignen würden sich hierfür ein schallisolierter Meßraum, der beiderseits über kleine Fenster zum Ein- und Austritt der Laserstrahlen verfügt, so daß alle optischen Teile der Anordnung außerhalb des Einflußbereiches des Schallfeldes stehen. Das zu realisieren, war uns leider nicht möglich.
Ebenso wie bei der Längenmessung ist es auch bei der Geradheitsmessung erforderlich, sich mit der statistischen Schwankung der Meßwerte zu befassen. Um die Messungen nicht durch die sich bei abgeschalteter Klimaanlage ausbildende Temperaturschichtung, die, begründet durch die großen Standartabweichungen der Meßwerte, selbst schon fast statistischen Charakter hat, zu beeinflussen und um dem Einsatz des Laserwegmeßsystems in Werkstätten und Maschinenhallen Rechnung zu tragen, wurden die Messungen der statistischen Schwankungen der Meßwerte bei laufender Klimaanlage durchgeführt. Dazu fand ein Versuchsaufbau nach Bild 4.3.8 Verwendung, bei dem die Höhe z = 120 cm für alle Versuche einheitlich war.

Bild 4.3.8: Anordnung zur Messung der statistischen Schwankungen des Geradheitsmeßwertes; die optischen Komponenten sind mit denen des Bildes 2.2.7 identisch; es bezeichnen z die Höhe des aus dem Laser austretenden Strahls über dem Fußboden, x die Länge der Meßstrecke und r den Abstand der Meß- und Referenzstrahlen
Gemessen wurden innerhalb der Meßzeit t und der Entfernung x jeweils 32768 Werte, deren empirische Standartabweichungen mit dem Programm "zlm-stat" gewonnen wurden. Sie sollen als Maß für den Meßfehler gelten und sind in Tabelle 4.3.9 dargestellt.
| x in m | |||||
| t in s | 1,00 | 2,00 | 3,20 | 4,00 | Mittel |
| 3,3 | 0,165 | 0,118 | 0,171 | 0,090 | 0,136 |
| 6,7 | 0,188 | 0,219 | 0,129 | 0,186 | 0,180 |
| 13,4 | 0,123 | 0,242 | 0,188 | 0,309 | 0,215 |
| 26,8 | 0,188 | 0,210 | 0,293 | 0,267 | 0,239 |
| 53,6 | 0,142 | 0,260 | 0,248 | 0,210 | 0,215 |
| 107,4 | 0,164 | 0,253 | 0,262 | 0,254 | 0,233 |
| Mittel | 0,153 | 0,212 | 0,200 | 0,206 | 0,203 |
Vor Beurteilung dieser Werte ist es jedoch erforderlich, sich über den Einfluß der statistischen Brechzahlschwankungen und damit der optischen Weglängen des Meß- bzw. Referenzarms Gedanken zu machen. Dazu können nicht die Ergebnisse der Messungen des Kapitels 4.1.2.2 genutzt werden, da sie unter Verwendung eines Meß-Referenz-Strahlenabstands von 4 cm gemessen wurden. Die Abstände der Meß- und Referenzstrahlen der Anordnung nach Bild 4.3.8 betragen jedoch nur r = 1,5 cm. Deshalb wurden Messungen der statistischen Schwankungen des Geradheitsmeßwertes durchgeführt, wobei die Doppelkeilprisma-Winkelspiegelkombination durch einen Planspiegel ersetzt wurde (Bild 4.3.10). Die analog zu den Werten der Tabelle 4.3.9 gewonnenen Resultate sind in Tabelle 4.3.11 dargestellt.

Bild 4.3.10: Anordnung zur Messung der statistischen Schwankungen des Geradheitsmeßwertes, verursacht durch Schwankungen des Brechungsindex längs der Meß- und Referenzstrahlen
| x in m | |||||
| t in s | 1,00 | 2,00 | 3,20 | 4,00 | Mittel |
| 3,3 | 0,198 | 0,057 | 0,087 | 0,183 | 0,131 |
| 6,7 | 0,045 | 0,067 | 0,051 | 0,274 | 0,109 |
| 13,4 | 0,155 | 0,082 | 0,062 | 0,299 | 0,150 |
| 26,8 | 0,134 | 0,190 | 0,057 | 0,205 | 0,146 |
| 53,6 | 0,164 | 0,081 | 0,096 | 0,286 | 0,157 |
| Mittel | 0,139 | 0,096 | 0,071 | 0,249 | 0,139 |
Die in Tabelle 4.3.11 angegebenen Werte als auch ihre Mittelwerte zeigen weder gegen die Meßzeit noch gegen die Meßentfernung ein monotones Verhalten, was nur durch den Einfluß der Klimaanlage (hohe Geschwindigkeit und geringe Größe der Turbulenzelemente) begründet werden kann. Dadurch entfällt die Weg- und Zeitabhängigkeit und damit auch die Notwendigkeit einer Betrachtung nach Gl. (4.1.4) bzw. (4.1.5). Die empirische Standardabweichung sD der Geradheitsmeßwerte als reine Folge der Schwankung der Differenz der optischen Weglängen von Meß- und Referenzarm kann daher als konstanter Wert
| (4.3.9) |
angegeben werden. Diese wollen wir nun mit den in Tabelle 4.3.9 dargestellten Resultaten vergleichen.
Die in Tabelle 4.3.9 dargestellten Meßwerte zeigen ebenfalls keine Monotonie. Entsprechend der in vorhergehenden Absatz angeführten Begründung genügt es auch hier, den zeit- und wegunabhängigen Gesamtmittelwert
| (4.3.10) |
zu betrachten. Aus den durchgeführten Messungen sollten sich eigentlich nach Gl. ( 3.4.26) Rückschlüsse auf die mittlere Größe und Brechzahldifferenz der Turbulenzelemente schließen lassen. Das ist jedoch bei der im Vergleich zur Größe der Schwankung der Meßwerte geringen Meßwertanzahl nicht möglich. Dazu wäre eine viel höhere Meßwertanzahl (Faktor 10) und vor allen Dingen die Messung über größere Meßentfernungen und -zeiten notwendig. Dies zu realisieren scheiterte an der fertigungsbedingten schlechten Qualität der verwandten optischen Bauteile, die nur als Prototyp verfügbar waren.
Nach der zur Herleitung der Gl. (3.4.26) angegebenen Begründung der statistischen Unabhängigkeit, die natürlich auch für die Gln. (4.3.9) und (4.3.10) gilt, resultiert die Geradheitsabweichung des Laserstrahls nach
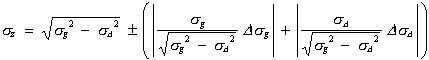 |
(4.3.11) |
zu
| (4.3.12) |
Als Meßunsicherheit der bei den Geradheitsmessungen gewonnenen Meßwerte muß natürlich Gl. (4.3.10) gelten, da letztlich beide Fehleranteile (4.3.9) und (4.3.12) in die Messungen eingehen. Dazu addiert sich noch das Inkrement des Meßsystems unter Berücksichtigung der verwandten Optik. Für die meisten Fälle ist das die Optik bis 2 m, deren Inkrement zg,ink,1= 0,12 mm beträgt. Die maximale Streubreite der Geradheitsmessung mit dieser Optik bei der Abnahme von Koordinatenmeßgeräten /3/ ergibt sich daraus zu
| (4.3.13) |
die der Abnahme von Werkzeugmaschinen /2/ zu
| (4.3.14) |
Messungen mit der Optik bis 10 m wurden nicht durchgeführt. Die von den Inkrementen unabhängigen Schwankungen der Strahlrichtung und der optischen Weglängen ändern sich dadurch nicht. Es würde höchstens eine Verfälschung durch das große Inkrement entstehen.
Damit soll die Untersuchung der physikalischen Grenzen beendet sein, wir wollen uns nun abschließend der Untersuchung einiger technischer Grenzen zur Herstellung der zur Geradheitsmessung genutzen optischen Bauteile zuwenden.
Die Fertigung von Optikteilen zur Weg- und Winkelmessung auch für heterodyn arbeitende Laserwegmeßsysteme gehört seit vielen Jahren zum Stand der Technik. Ebenso zum Stand der Technik gehört die auf dem Einsatz eines Wollaston-Prismas beruhende Optik zur Geradheitsmessung /19/. Die durch den Einsatz eines Doppelkeil-Prismas charakterisierte Geradheitsmeßoptik (Bild 2.2.7) ist zwar im Prinzip ebenfalls dem Stand der Technik zuzuordnen, ihre Serienfertigung im Hause "Carl Zeiss" stellt jedoch ein Novum dar. Deshalb soll sich die Untersuchung der technischen Grenzen bei der Messung geometrischer Größen auf die Untersuchung der fertigungstechnisch zu fordernden Toleranzen für die einzelnen Bauteile der Geradheitsmeßoptik beschränken, die den Schwerpunkt dieses Kapitels bildet.
Die Untersuchung der Winkelfehler bildet hierbei den Anfang. Fehler der Parallelität der Meß- und Referenzstrahlen a in der im Bild 5.1.1 dargestellten Ebene gehen bei der Bewegung des Doppelkeilprismas (Bild 2.2.7) um den Betrag x längs der Strahlen als lineare Fehler Dzg in den Meßwert der Geradheit ein. Ihre Größe berechnet sich zu
| (5.1.1) |
wobei der Nenner aus der Anzahl der Durchgänge (4) der Strahlen durch das Doppelkeilprisma und der Auswirkung auf nur einen Keil (2) des Prismas resultiert, und der Faktor n die Anzahl der nach Entstehen des jeweiligen Teilfehlers erfolgenden Transmissionen des Doppelkeiles berücksichtigt. Deshalb muß es nachfolgend darum gehen, den maximal erreichbaren, aus den einzelnen Fehlern resultierenden Parallelitätsfehler in der in Bild 5.1.1 gezeigten Ebene zu bestimmen. Parallelitätsfehler in der zum Bild 5.5.1 orthogonalen Ebene gehen nicht in den Fehler ein, da der Meßaufbau in dieser Ebene unempfindlich gegen Geradheitsabweichungen ist und das Dachkantprisma (Bild 2.2.7) kompensierend wirkt.
Nach Angabe von Teichmann, Carl Zeiss Jena, beträgt die unter marktbeständigen Kosten realisierbare Parallelität und Ebenheit der einzelnen Glasflächen lHeNe/20 » 32 nm jeweils über die Breite der gesamten Fläche bzw. den Strahlabstand betrachtet. Kittfehler entfallen, da alle Bauteile des Strahlteilers aneinander gesprengt sind.
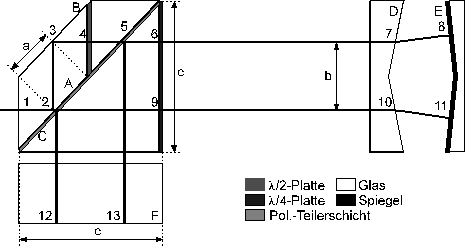
Diese Angaben sollen als Grundlage der Berechnung der einzelnen Parallelitätsfehler ai,j der Strahlen dienen, wobei sich die Indizes auf die in Bild 5.1 bezeichneten Punkte beziehen. Dazu betrachten wir nur die bei Reflexion an den einzelnen Flächen (Bild 5.1.1) entstehenden Fehler. Der bei der (vom Fehler abgesehen) senkrechten Transmission von Flächen bzw. Transmission von Planplatten entstehende Parallelitätsfehler kann vernachlässigt werden.
Kommen wir nun zur Betrachtung der einzelnen, durch o.g. Produktionstoleranz verursachten Fehler, die alle im durch die Punkte 1-2-3-4-5-6-7-8-7-6-5-13 und zurückführenden Strahl konzentriert sein sollen. Der durch die Punkte 1-2-9-10-11-10-2-12 und zurück führende Strahl soll als fehlerfrei gelten.
Der Parallelitätsfehler der Flächen A und B erzeugt den bei allen vier Durchgängen der Meß- und Referenzstrahlen durch den Doppelkeil vorhandenen Fehler der Stahlparallelität a2,3. Er beträgt entsprechend der aus der Kantenlänge c = 4 cm des Strahlteilers resultierenden perspektivischen Breite a = Ö2 cm der Parallelflächen
| (5.1.2) |
Die Reflexion an Fläche F, für die in Kombination mit Fläche D der gleiche Fehler gelten soll, verursacht mittels des Strahlabstandes b = 2 cm den bei drei Doppelkeildurchgängen wirksamen Fehler
| (5.1.3) |
Weiterhin entsteht bei der Reflexion an Fläche F und F' (zweite Ebene, vgl. Bild 2.2.7) der durch den Abstand b hervorgerufene, auf zwei Transmissionen des Doppelkeiles wirksame Fehler
| (5.1.4) |
Die Fehler der Reflexionen an der Fläche C vor bzw. nach Reflexion an Fläche F kompensieren einander. Beim nochmaligen Durchlauf der Punkte 7-8-7 entsteht ebenfalls der Fehler (5.1.3), der nur auf eine Doppelkeiltransmission wirkt. Durch Summation der einzelnen Anteile ergibt sich der Gesamtfehler
| (5.1.5) |
Experimentelle Messungen an der zur Verfügung stehenden Prototyp-Optik erbrachten folgende Ergebnisse: Der Fehler a2,3 wurde durch Messung des Auseinanderlaufes der Meß- und Referenzstrahlen nach Austritt (Punkte 6 und 9) aus dem Strahlteiler über eine Distanz von 10,5 m gemessen und ergab sich zu
| (5.1.2a) |
Der Winkel a7,8 resultiert aus der Messung mit einem Präzisionsgoniometer und beträgt für die Prototypen beider Meßentfernungen
| (5.1.3a) |
Ein Auftreten des Winkelfehlers a12,12' konnte experimentell nicht festgestellt werden. Entsprechend
Gl. (5.1.5) ergibt sich daraus der experimentelle Geradheitsfehler
| (5.1.5a) |
Gl. (5.1.5a) ist eine Gerade im zg-x-Diagramm. Daher eliminiert sich dieser Fehler bei Berechnung der Geradheitsabweichungen gegen die numerische Ausgleichsgerade durch die Meßwerte. Weil der Fehler (5.1.5a) aber zwischen Meß- und Referenzstrahl entsteht, läßt er sich nicht durch geeignete Justage (vgl. Kap. 5.3) ausgleichen. Das bedeutet, daß sich der in den Laserkopf zurückgeworfene Meßstrahl nicht mehr vollständig mit dem Referenzstrahl deckt, der Strahlversatz Dzs beträgt
| (5.1.6) |
Die direkte experimentelle Überprüfung ergab
| (5.1.7) |
Darüber hinaus besitzen Meß- und Referenzstrahl bei Eintritt in den Laserkopf den in Gl. (5.1.5a) als Vorfaktor enthaltenen Winkelfehler. Das führt zu Problemen bei der Einkopplung der Strahlen in den Meßlichtwellenleiter (vgl. Kap. 2.1), die, zusammen mit den in Kap. 5.2 angegebenen Fehlern, dazu führten, daß Messungen nur bis zu einer Entfernung des Winkelspiegels vom Strahlteiler von fünf Metern möglich waren.
Abschließend sind noch einige Bemerkungen zum Winkelfehler a7,8 notwendig. Entsprechend den Konstruktionsunterlagen von Teichmann ist nicht der Keilwinkel k (Bild 2.2.8), sondern der Ablenkwinkel f der Doppelkeilprismen angegeben. Er ist die zum von den Spiegelflächen eingeschlossenen Winkel zugeordnete, brechzahlunabhängige Größe, während der Keilwinkel k von der von Glascharge zu Glascharge differierenden Brechzahl des verwandten BK7-Glases abhängt. Unserer Ansicht nach ist es trotzdem sinnvoller, hier den Keilwinkel k anzugeben, da er der körperlich zu fertigende und somit produktionstechnisch relevante Winkel ist. Dazu muß die Brechzahl eines ausgewählten Glasblocks gemessen und der passende Keilwinkel berechnet werden. Dieser Glasblock ist dann nur für die Produktion der Doppelkeilprismen zu verwenden. Eine Alternative besteht in der Vermessung jeder einzelnen Charge und der individuellen Berechnung des Keilwinkels.
Die Funktionsweise des Strahlteilers beruht im wesentlichen auf der Ebenheit der Polarisationsrichtungen der beiden Lasermoden (vgl. Kap. 2.2.3). Die daraus unmittelbar resultierenden Meßfehler sollen hier nicht untersucht werden. Tiefer gehende Aussagen dazu finden sich in /11/.
Die ordnungsgemäße Einhaltung der Polarisationebenen ist Voraussetzung für die Funktion der als Lichtventil wirkenden Kombination der beiden Phasenverzögerungsplatten und der Polarisationsteilerschicht. Überschreitet der Fehler der Polarisationsebenen einen bestimmten Betrag, so werden nicht alle nach der ersten Reflexion am Spiegel zurückkommenden Strahlanteile an der Polarisationsteilerschicht reflektiert. Es kommt zu Rückkopplungen in den Laserresonator, in deren Folge die Wellenlängen des Lasers instabil werden und eine korrekte Messung nicht mehr möglich ist.
Experimentelle Untersuchungen der Fehlerkomponenten der Polarisation ergaben ein Intensitätsverhältnis Intensität in der geforderten Polarisationebene zu ihrer orthogonalen Fehlerkomponente von 100:1. Daraus resultierend mußte die Versuchsanordnung nach Bild 2.2.7 immer leicht dejustiert werden. Nur so konnten zu hohe Rückkopplungen in den Laser verhindert werden. Das hatte einen Winkelfehler und einen zusätzlichen Parallelversatz der in den Laserkopf zurückgeworfenen Strahlen (Bild 2.1.2) zur Folge, der ursächlich die Einkoppelung eines genügend großen Strahlungsflusses beider Moden in den Meßlichtwellenleiter verhinderte.
Die zur Umwandlung des optischen in ein elektrisches Signal genutzten Avalche-Dioden (Kap. 2.1) und deren nachgeschaltete Trigger zur Ansteuerung des Zählers benötigen zum ordnungsgemäßen Betrieb eine absorbierte (mittlere) Grundleistung und eine absorbierte mittlere Heterodynleistung des 640MHz-Signals. Diese konnte in Folge der notwendigen Dejustierungen und der im Kap. 5.1 beschriebenen Fehler nicht immer aufgebracht werden. Bei Meßentfernungen größer fünf Meter begann der Zähler in statistischen Zeitabständen um mehrere Inkremente zu springen. Deshalb waren Messungen über größere Meßentfernungen nicht möglich.
Justierfehler sind eine der häufigsten Fehlerquellen in der wegmessenden Interferometrie. An dieser Stelle sei nur auf die Bedeutung des Cosinusfehlers /4/ verwiesen. Deshalb ist es notwendig, über ihren Einfluß auf die Geradheitsmessungen nachzudenken.
Die Betrachtung der Justierfehler soll einhergehend mit einer Justieranleitung gegeben werden. Sie beinhaltet die folgenden Punkte:
| (5.3.1) |
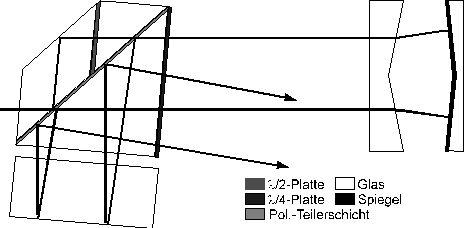
Bild 5.3.1: Strahlverlauf an der Geradheitsoptik bei mangelhafter Justierung des Strahlteilers
Daraus folgernd ist eine sehr feinfühlige Justierung des Strahlteilers erforderlich. Hier ist die Entwicklung einer Feinjustierung erforderlich, die entweder den gesamten Strahlteiler oder nur das am Strahlteiler befestigte Dachkantprisma um eine zur Ebene des Bildes 5.3.1 senkrechte Achse dreht. Die reine Drehung des Dachkantprismas ist möglich, da ein konstanter Parallelversatz der Meß- und Referenzstrahlen die Meßwerte nicht beeinflußt. Ein verbleibender, visuell nicht mehr kontrollierbarer Winkelfehler erzeugt einen Cosinusfehler, der vermittels der Regressionsgerade kompensiert wird.
Entsprechend dem Hauptschwerpunkt der Diplomarbeit sollen nachfolgend kurz die Ergebnisse der Untersuchungen zur Geradheitsmessung wiedergegeben werden, eine Zusammenfassung der gleichzeitig gewonnenen Ergebnisse zur Winkel- und Längenmessung erfolgt nicht.
Die durch Einflüsse der Gravitation auf die Wellenlänge des Lichtes
| (3.2.8) |
als auch auf die Geradheitsabweichung des Laserstrahls
| (3.2.12b) |
verursachten Abweichungen liegen mehrere Größenordnungen unter der Auflösung des Meßsystems. Sie müssen daher nicht berücksichtigt werden. Der durch die nichtrelativistische Näherung des Dopplereffekts verursachte Fehler (2.3.18) hat ebenfalls keine Auswirkungen auf das Meßergebnis.
Einen weiteren Untersuchungsgegenstand bildeten die Einflüsse der atmosphärischen Umwelt. Dazu wurde festgestellt, daß die Luftbrechzahl der Berücksichtigung in der Meßgleichung der Geradheit
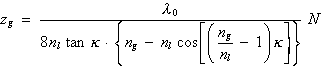 |
(3.3.5) |
bedarf. Die aus den Meßunsicherheiten der Brechzahlparameter der Edlén-Gleichung (3.3.1) resultierenden Meßunsicherheiten der Brechzahl haben den vernachlässigbaren Einfluß
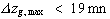 |
(3.3.12) |
auf das Meßergebnis.
Ebenfalls vernachlässigbar sind die infolge der Absorption und Streuung auftretende Schwächung des Strahlungsflusses (3.3.18) des Strahls und dessen thermische Eigendefokussierung (3.3.45). Derartige Probleme traten auch bei den experimentellen Arbeiten nie auf.
Ganz anders verhält es sich mit der Ausbreitung des Laserstrahls in einer Umgebung kontinuierlich veränderlicher Temperatur. Hier konnte die theoretisch ermittelte Geradheitsabweichung
| (3.3.30a) |
punktuell im Experiment (Kap. 4.3.1) bestätigt werden. Zu einer exakten Überprüfung des funktionellen Zusammenhanges (3.3.30a) fehlten leider die Mittel und Möglichkeiten.
Die experimentelle Überprüfung des Einflusses eines auf den Laserstrahl einwirkenden Druckgefälles, das die Geradheitsabweichung
| (3.3.48a) |
verursacht, konnte nicht erfolgen, da sich der dazu erforderliche, statische Druckgradient nicht realisieren ließ. Anstelle der Gleichung (3.3.48a) wurde aber die darauf beruhende Beziehung für die Anhängigkeit der Amplitude der Geradheitsabweichung von Schallwellen
| (3.3.56) |
überprüft. Ihre Gültigkeit ergab sich im Rahmen der allerdings mit einem hohem Fehler ( D(Dz) » 25% ) behafteten Meßwerte für mehrere Schalldruckpegel und -frequenzen.
Daraus resultierend kann die durch statische Umwelteinflüsse hervorgerufene Geradheitsabweichung
| (3.3.63) |
bzw. deren Differenz zur Regressionsgerade durch Gl. (3.3.63)
| (3.3.72) |
mit
| (3.3.63a) |
als experimentell bestätigt angesehen werden.
Die Untersuchung der statistischen atmosphärischen Einflüsse auf die Geradheitsmessung bildete einen weiteren Schwerpunkt der Arbeit. Die auf der Existenz von Turbulenzelementen beruhende theoretische Erwartung der mittleren Schwankungen des Geradheitsmeßwertes wurde experimentell nicht hinreichend bestätigt. Die als Meßunsicherheit in den Gln. (4.3.2) und (4.3.3) angegebene empirische Standardabweichung bei angeschalteter Klimaanlage lag zwar innerhalb des durch
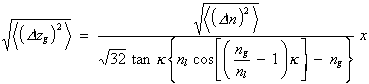 |
(3.4.25) |
gegebenen Bereiches, jedoch ist dieser Bereich durch die unbekannte Größe der Turbulenzelemente (3.4.5) und die unbekannte Größe der mittleren Brechzahlschwankungen (3.4.4) so groß, daß eine Gl. (3.4.25) bestätigende Interpretation sehr vage wäre. Der Versuch der Einschränkung des Schwankungsbereiches der Brechzahlen durch seine Bestimmung aus experimentellen Schwankungen der Entfernungsmeßwerte nach Gl. (3.4.21) scheiterte, da die Gültigkeit der Gl. (3.4.21) nicht bestätigt werden konnte. An deren Stelle ergab sich ein empirischer, auf einem ergodischen Raum-Zeit-Kontinuum beruhender Zusammenhang (4.1.4), der aber keine Rückschlüsse auf Gl. (3.4.4) zuließ und somit den Definitionsbereich der Gl. (3.4.25) nicht einschränkte. An dieser Stelle sind umfassendere theoretische und experimentelle Untersuchungen notwendig, die einerseits auf eine Untersuchung des Zusammenhangs (3.4.25) und andererseits auf eine Klärung des Widerspruches zwischen den theoretisch motivierten Resultaten der Turbulenztheorie (3.4.21) und dem nach den ergodischen Raum-Zeitansatz (4.1.4) erklärbaren experimentellen Ergebnissen ausgerichtet sind.
Die theoretisch nicht motivierte, experimentell für Meßentfernungen bis zu vier Metern ermittelte, statistische Meßunsicherheit (empirische Standardabweichung) der Geradheitsmeßwerte beträgt
| (4.3.10) |
und wird wegen zu gleichen Teilen (je 70% des Wertes (4.3.10)) durch Schwankungen der Brechzahldifferenz längs der Meß- und Referenzstrahlen und durch Schwankungen der Geradheit der Strahlen verursacht. Die aus Gl. (4.3.10) resultierenden Streubreiten zur Abnahme von Koordinatenmeßgeräten /3/ bzw. Werkzeugmaschinen /2/ ergeben sich zu
| (4.3.13) |
bzw.
| (4.3.14) | |
| (3.5.10) |
Fehlerverursachend wirkt sich auch das heterodyne Meßprinzip des ZLM 300 aus. Die Fehler entstehen dabei nicht durch Bewegungen des Doppelkeilprismas (Bild 2.2.7) längs der Meßgerade, sondern durch Querbewegungen. Die dabei entstehende optische Weglängendifferenz hat im Meß- und im Referenzstrahl zwar den gleichen Betrag (unterschiedlichen Vorzeichens), aber die resultierenden Zählerwerte unterscheiden sich wegen der differierenden Wellenlängen etwas. Der dadurch verursachte Fehler
| (3.5.10) |
besitzt unter Berücksichtigung der maximal meßbaren Geradheitsabweichung
| (3.5.11) |
Er kann wegen seiner Kleinheit zum Geradheitsinkrement vernachlässigt werden.
Letztlich beeinflussen die fertigungstechnischen Grenzen die Meßgenauigkeit des Laserwegmeßsystems. Der durch die maximal erreichbare Ebenheit und Parallelität und die daraus begrenzte Maßhaltigkeit der Winkel der Meßoptik verursachte Fehler hat die vom zurückgelegten Weg des Doppelkeilprismas abhängige maximale Größe
| (5.1.5) |
Der Fehler des verwendeten Prototyps ist mit
| (5.1.5a) |
um etwa eine Größenordnung schlechter. Hier Bedarf es also dringend einer exakteren Fertigung.
Für die Anforderung an die Polarisationsoptik gilt das Erfordernis der exakteren Fertigung in gleicher Weise. Das am Prototyp gemessene Verhältnis der Intensität in der jeweils geforderten Ebene zu ihrer Fehlerkomponente der orthogonalen Ebene beträgt etwa 100:1. Hier ist eine technisch durchaus realisierbare Steigerung auf mindestens 1000:1 erforderlich.
Die aus der nie exakt realisierbaren Justierung folgenden Fehler kompensieren sich alle dadurch, daß ihre zum zurückgelegten Weg des Doppelkeilprismas linearen Größen in der Berechnung des Anstiegs der Ausgleichsgerade, gegen die die Geradheitsabweichungen angegeben werden, enthalten sind. Die gegen diese Ausgleichsgerade korrigierten Meßwerte bleiben von den Justierfehlern unbeeinflußt.
| /1/ | Schüßler, H. H. |
Prinzip, technische und wirtschaftliche Bedeutung der
Laserinterferometrie. Vortrag, Laserinterferometrie in der Längenmeßtechnik,
Handbuch zum Seminar der VDI/VDE-Gesellschaft für Meß- und
Automatisierungstechnik vom 12./13.11.1990 in Stuttgart, VDI Bildungswerk, Düsseldorf 1990 |
| /2/ | Norm | VDI/VDE 3441: Statistische Prüfung der Arbeits- und Positioniergenauigkeit von Werkzeugmaschinen. Beuth, Berlin 1986 |
| /3/ | Norm | VDI/VDE 2617: Genauigkeit von Koordinatenmeßgeräten. Beuth, Berlin 1986 |
| /4/ | Hoffer, T. M. Fischer, W. |
Abnahme von Werkzeugmaschinen mit einem Laser-Meßsystem, Teil 1 u.2. Feinwerktechnik und Meßtechnik 85(1977) 6 , S. 229-284 und 85(1977) 7, S. 343-353 |
| /5/ | Kasparick, B | Laserinterferometer als Einbauwegmeßsysteme in Werkzeugmaschinen und Koordinatenmeßgeräten. Vortrag, Laserinterferometrie in der Längenmeßtechnik, Handbuch zum Seminar der VDI/VDE-Gesellschaft für Meß- und Automatisierungstechnik vom 12./13.11.1990 in Stuttgart, VDI Bildungswerk, Düsseldorf 1990 |
| /6/ | Luhs, W. | Aufbau und Funktionsweise von Laserinterferometersystemen. Vortrag, Laserinterferometrie in der Längenmeßtechnik, Handbuch zum Seminar der VDI/VDE-Gesellschaft für Meß- und Automatisierungstechnik vom 29./30.10.1991 in Düsseldorf, VDI Bildungswerk, Düsseldorf 1991 |
| /7/ | Autorenkollektiv | Wissensspeicher Lasertechnik. VEB Fachbuchverlag, Leipzig 1982 |
| /8/ | Kleen, W. Müller, R. |
Laser. Springer Verlag, Berlin 1988 |
| /9/ | Prospekt | Frequenzstabilisierter HeNe-Laser - Laser HN 26 ST/1 der Jenoptik GmbH. Jena 1992 |
| /10/ | Bennett, S. J. Wilson, D. C. |
Stabilised Laser. Patentschrift GB 1 448 676 vom 18.02.74 |
| /11/ | Walke, M. | Theoretische und experimentelle Untersuchungen von systematischen Fehlern in einem Zweifrequenz-Laserinterferometer-Wegmeßsystem im Produktionsbereich Optische Meßtechnik der Carl-Zeiss-Jena GmbH. Diplomarbeit, Friedrich-Schiller-Universität Jena 1992 |
| /12/ | Müller, J. Chour, M. |
Zweifrequenz-Laserwegmeßsystem für extreme Verfahrgeschwindigkeiten und hohe Genauigkeit. Technisches Messen 58 (1991) 6, S.253-256 |
| /13/ | Chour, M. Netzel, M. |
Stehwelleninterpolator. Patentschrift DD 296 549 A5 vom 05.12.91 |
| /14/ | Wayne Kenneth, J. | Plane mirror interferometer. Patentschrift EP 0 281 385 A3 vom 02.03.88 |
| /15/ | Young, P. S. Sommargren, G. E. |
Differential plane mirror having beamsplitter/beam folder assembly. Patentschrift US 4 802 765 vom 07.02.89 |
| /16/ | Chour, M. Netzel, M. |
Symmetrisches Trägerfrequenzinterferometer. Patentschrift DD 292 696 A5 vom 08.08.91 |
| /17/ | Sommargren, G. E. | Angle measuring interferometer. Patentschrift EP 0 244 275 A2 vom 16.03.87 |
| /18/ | Ohlenbusch, J. | Einrichtung zum Messen von Längen und Winkeln mit einem Interferometer. Patentschrift DE 3 830 962 C2 vom 01.07.1993 |
| /19/ | Baldwin, R. R. | Interferometer system for measuring straightness and roll. Patentschrift US 3 790 284 vom 05.02.74 |
| /20/ | Schüßler, H.H. | Anordnung, Variation und Ausrichtung von Laserinterferometer-Komponenten. Vortrag, Laserinterferometrie in der Längenmeßtechnik, Handbuch zum Seminar der VDI/VDE-Gesellschaft für Meß- und Automatisierungstechnik vom 29./30.10.1991 in Düsseldorf, VDI Bildungswerk, Düsseldorf 1991 |
| /21/ | Fürst, A. | Bedienungsanleitung des Ebenheitsmeßprogrammes "PC_EBE". Version 2/7-92, Gesellschaft für Meßtechnik mbH, Hirzenrott2, Aachen 1992 |
| /22/ | Klein, M. V. Furtak, T. E. |
Optik. Springer Verlag, Berlin, Heidelberg, New York, Tokyo, 1988 |
| /23/ | Tschach, F. | Längenmessung mit integrierter Temperaturkorrektur. Feingerätetechnik 38 (1989) 6, S. 246-249 |
| /24/ | Tschach, F. | Die Temperatur als Störungsquelle in der Präzisionsmeßtechnik. Feingerätetechnik 34 (1985) 10, S. 448-450 |
| /25/ | Tyler Estler, W. | Calibration and use of optical straightedges in the metrology of precision machines. Optical Engineering 24 (1985) 3, S. 372-379 |
| /26/ | Tanimura, Y. Fujinuma, N. Sakurai, Y. |
Error Factors and Measuring Accuracy in Lenght Measurement with Laser Interferometer. Bull. Japan Soc. of Pec. Engg. 14 (1980) 3, S. 187-201 |
| /27/ | Obuchow, A.M. | Über den Einfluß schwacher Inhomogenitäten der Atmosphäre auf die Schall- und Lichtausbreitung. Sammelband zur statistischen Theorie der Turbulenz, Herausgeber: Goering, H., Akademie-Verlag, Berlin 1958 |
| /28/ | Trapet, E. | Ein Beitrag zur Verringerung der Meßunsicherheit von Fluchtungsmessystemen auf Laserbasis. Dissertation, Technische Hochschule Aachen, 1982 |
| /29/ | Steimetz, C. Burgoon, R. Herris, J. |
Accuracy Analysis and Improvements to the Hewlett-Packard Laser Interferometer System. Interferomatric Metrology, Critical Reviews of Optical Science and Technology, N.A.Massie, Editor, SPIE 816 (1988), S. 79-91 |
| /30/ | Sexl, R. und H. | Weiße Zwerge - Schwarze Löcher. Friedr. Vieweg & Sohn Verlagsgesellschaft mbH, Braunschweig 1979 |
| /31/ | Schmutzer, E | Grundlagen der theoretischen Physik. VEB Deutscher Verlag der Wissenschaften, Berlin 1989 |
| /32/ | Schmutzer, E. | Relativistische Physik. B. G. Teubner Verlag, Leipzig 1968 |
| /33/ | Prospekt | Laserwegmeßsystem ZLM 300. Carl Zeiss Jena GmbH, Produktbereich Optische Meßtechnik, Tatzendpromenade 1a, Jena 1992 |
| /34/ | Edlén, B. | The Refractiv Index of Air. Metrologia 2 (1966) 2, S.71-80 |
| /35/ | Birch, K. P. Downs, M. J. |
The results of a comparison between calculatet and measured values of therefractiv index of air. Journal of Physical Engineering 21 (1988)7, S. 694-695 |
| /36/ | Wilkening, G. | Kompensation der Luftbrechzahl. Vortrag, Laserinterferometrie in der Längenmeßtechnik, Handbuch zum Seminar der VDI/VDE-Gesellschaft für Meß- und Automatisierungstechnik vom 29./30.10.1991 in Düsseldorf, VDI Bildungswerk, Düsseldorf 1991 |
| /37/ | Prospekt | Automatischer Umweltkompensator. Carl Zeiss Jena GmbH, Produktbereich Optische Meßtechnik, Tatzendpromenade 1a, Jena 1992 |
| /38/ | Prospekt | High performance motion control for precision equipment, HP 5527B Laser Position Transducer System. Hewlett-Packard Company, 5301 Stevens Creek Blvd., Santa Clara 1990 |
| /39/ | Prospekt | Laserinterferometer ZLI 150. Spindler & Hoyer GmbH,Königsallee 23, Göttingen, 1991 |
| /40/ | Sommergreen, G. E. | A new laser measurement system for precision metrology. Precision Engineering 9 (1987) 4, S. 179-184 |
| /41/ | Schüßler, H.H. | Die Eignung von Laser-Strahl und photoelektrischen Detektoren zur Messung der Abweichung von der Geradlinigkeit und Ebenheit im Maschinenbau. Dissertation, Technische Hochschule Aachen, 1971 |
| /42/ | Sommerfeld, A. | Vorlesungen über Theoretische Physik. Band IV: Optik, Verlag Harri Deutsch, Thun 1989 |
| /43/ | Bronstein, I.N. Semendjajew, K.A. |
Taschenbuch der Mathematik. BSB B. G. Teubner Verlagsgesellschaft, Leipzig 1987 |
| /44/ | J.W. Strohbehn u.a. |
Laser Beam Propagation in the Atmosphere. Serie: Topics in Applied Physics - Bd. 25, Springer-Verlag, Berlin - Heidelberg - New York 1978 |
| /45/ | Mende, R. Simon, G |
Physik - Gleichungen und Tabellen. VEB Fachbuchverlag Leipzig, Leipzig 1983 |
| /46/ | Lehrgangshandbuch | Technische Maßnahmen gegen Maschinenlärm. VDI-Bildungswerk, Düsseldorf, 1967 |
| /47/ | Hodara, H. | Laser Wave Propagation Through the Atmosphere. Proceedings of the IEEE 54 (1966) 3, S. 368-375 |
| /48/ | Tatarski, V. I. | Wave Propagation in a Turbulent Medium. Mc.Graw-Hill Verlag, New York 1961 |
| /49/ | N. Bobroff | Residual errors in laser interferometry from air turbulence and nonlinearity. Applied Optics 26 (1987) 13, S. 2676-2682 |
| /50/ | R. Gruß | Übertragung von Laserstrahlen durch die Atmosphäre. Nachrichtentechnische Zeitung 9 (1969) 3, S. 184-192 |
| /51/ | N. Edwards R. Steen |
Effects of Atmospheric Turbulence on the Transmission Visible and Near Infrared Radiation. Applied Optics 4 (1965) 3, S.311-316 |
| /52/ | A.L. Buck | Effects of the Atmosphere on Laser Beam Propagation. Applied Optics 6 (1967) 4, S. 703-708 |
| /53/ | Höhn, D. H. | Einfluß der Öffnungen an Quelle und Empfänger auf die terrestrische Intensitätsszintillatin. Optik 22 (1965) 9, S. 637-644 |
| /54/ | Hofmann, C. | Die optische Abbildung. Akademische Verlagsgesellschaft Geest & Portig K.-G., Leipzig 1980 |
| /55/ | Hart, H. | Einführung in die Meßtechnik. VEB Verlag Technik, Berlin 1987 |
| /56/ | Geilen, J. Quirin, K. |
Untersuchungen zur Richtungsstabilität von HeNe-Lasern mit Hilfe von elektronischen Meßlatten. Dissertation, Technische Hochschule Aachen, 1971 |
Für das fördernde Interesse am Fortgang dieser Arbeit danke ich Herrn Dipl.-Ing. Matthias Chour und Herrn Dr.-Ing. Dipl.-Phys. Jochen Müller, die gern bereit waren, mir ihr fachliches Wissen und ihre praktischen Erfahrungen zu vermitteln. Mein besonderer Dank gilt Herrn Prof. Dr. rer. nat. habil. Christian Hofmann für seine kritischen Hinweise bei der Anfertigung dieser Arbeit.
Ich erkläre, daß ich die vorliegende Diplomarbeit selbständig angefertigt und nur die angegebenen Hilfsmittel und Quellen verwendet habe
Jena, November 1993
Ralf Arnold