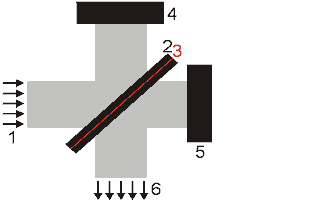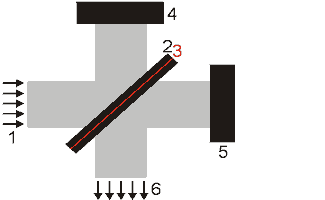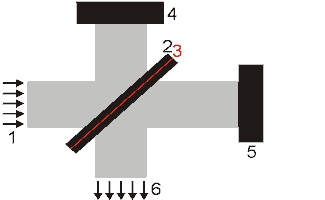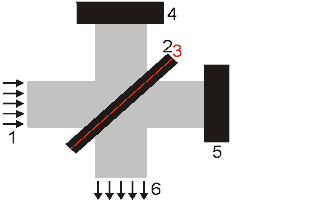
Ein Interferometer ist ein optischer Aufbau, der dazu dient, Lichtbündel (Wellen) zu trennen, sie räumlich gegeneinander zu verschieben und wieder zu überlagern.
Das einfachste bekannte Interferometer ist das Michelson-Interferometer. Das einfallende, parallele Lichtbündel 1 wird an der aktiven Schicht 3 eines Strahlteilers 2 in zwei (am besten gleich intensive) Teile aufgespalten. Ein Teil reflektiert am Stahlteiler zu einem fest stehenden Spiegel 4 (in den Referenzarm des Interferometers). Der andere Teil transmittiert zu einem bewegten Spiegel 5 (in den Meßarm). Beide Teile werden am jeweiligen Spiegel zum Strahlteiler zurück reflektiert und wiedervereinigt. Endsprechend der Position des beweglichen Spiegels besitzen beide Teilbündel eine Laufzeit- bzw. Wegdifferenz.
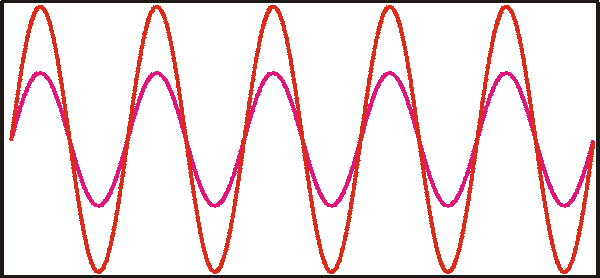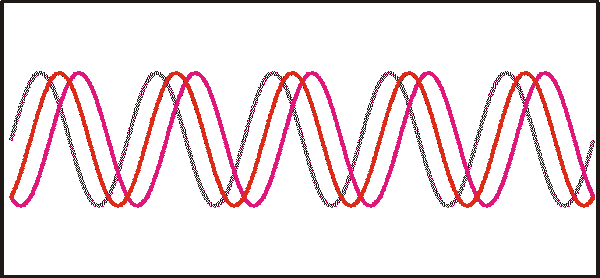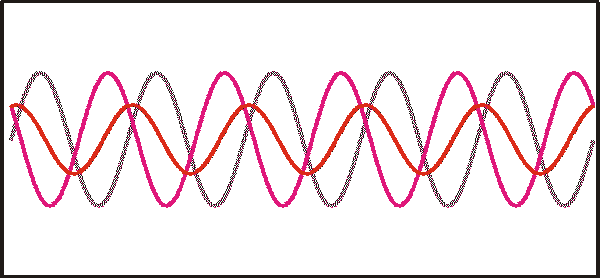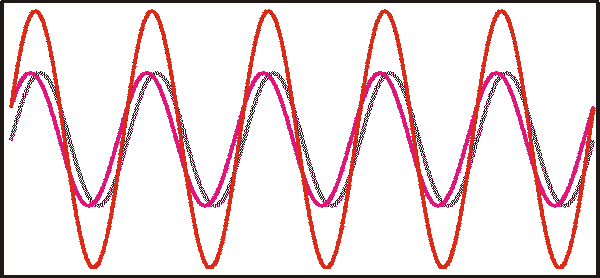
Obenstehende Grafik zeigt die Lichtwellen beider Teilbündel beim Verlassen des Interferometers bei festgehaltener Zeit und verändelichem Ort. Die aus dem Referenzarm kommende Welle (grau) ändert sich nicht. Aus der Bewegung des Spiegel folgernd, verschiebt sich die aus dem Meßarm kommende Welle (violett) gegen die des Referenzarms. Beide Wellen interferieren (überlagern sich) zu einer resultierenden Welle (rot). In Fall der optischen Weglängendifferenz null beider Armeüberlagern sich beide Wellen so konstruktiv, sie verstärken sich. Entspricht die optische Weglängendifferenz genau einer halben Lichtwellenlänge (Spiegelverschiebung um eine Viertelwellenlänge), so erfolgt die Überlagerung destuktiv (Auslöschung). Das das Interferometer verlassende Licht schwankt daher cosinusförmig über der Spiegelverschiebung.
Setzt man einen Detektor an einen festen Ort und registriert das Intensitätssignal, so nimmt der Detektor die Cosinusfunktion der Interferenz auf. Diese wird mathematisch durch folgende Gleichung beschrieben:
Hierin sind l die Wellenlänge und x die Weglängendifferenz. Unter Berücksichtigung, daß die Weglängendifferenz dem doppelten Spiegelweg X und die Wellenlänge dem Kehrwert der Wellenzahl ![]() entspricht, ergibt sich
entspricht, ergibt sich
![]()
Da Spektrometer Licht vieler Wellenlängen verarbeiten, entsteht die oben beschriebene Interferenz für jede Wellenlänge. Entsprechend überlagern sich die Interferenz-Intensitäten der einzelnen Wellenlängen zusätzlich.
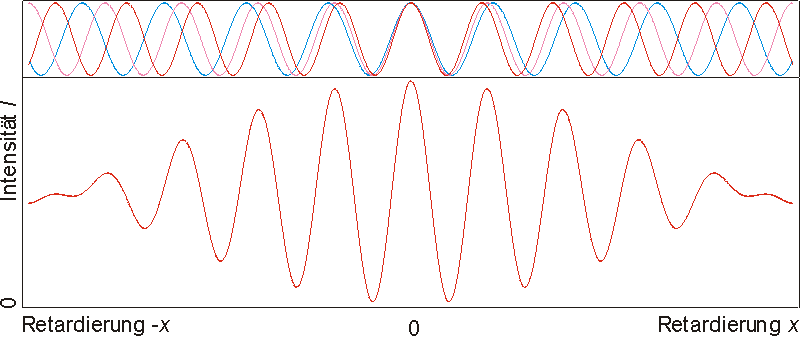
Eine solche Überlagerung als Summation für drei verschieden Wellenlängen (im Bild, oben) ergibt den im unteren Bild dargestellten Intensitätsverlauf als Funktion der Spiegelverschiebung. Der Nullpunkt des Spiegelwegs (x=0) ist der Ort an dem beide Interferometerarme gleich lang sind. Dort besitzen alle Wellen die Phasendifferenz Null und überlagern sich deshalb konstruktiv. Die Intensität ist maximal. Für zunehmende Spiegelwege unterscheiden nehmen die Phasendifferenzen der einzelnen Wellenlängen unterschiedlich stark, sie addieren sich nicht mehr zum Maximalwert.
Überlagert man alle Wellenlängen (Kontinuum) des an der Messung beteiligten Lichts, ergibt sich die vom Detektor erfaßte Intensität; als Integral über die Bandbreite B der Anordnung. Bei großen Spiegelverschiebungen sind die Phasen der einzelnen Wellenzüge nahezu gleichmäßig verteilt, sie addieren sich zu einem Mittelwert. Dieser Mittelwert enthällt keine spektroskopisch relevante Information. Der Mittelwert oder Gleichanteil des Interferogramms wird elektronisch herausgefiltert. Nur die Abweichung vom Mittelwert wird erfaßt und weiter betrachtet. Es ergibt sich für die am Detektor einfallende Intensität als Funktion des Spiegelwegs x
![]()
Ein mit einem IR-Spektrometer aufgenommes Interferogramm hat deshalb typischerweise folgende Form:
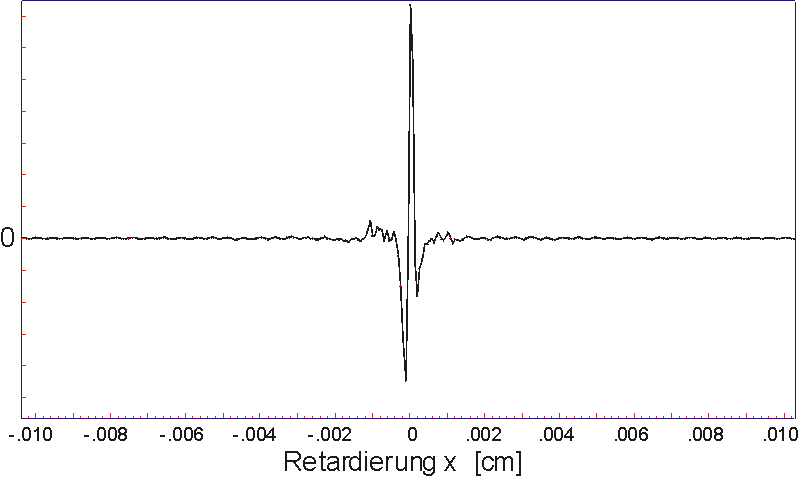
Betrachten wir sich die bereits oben angeführte Gleichung zur Berechnung der Interferenzintensität einer polychromatischen Interferenz
![]()
Diese kann man auch darstellen als Integral über den unendlichen Wellenzahlbereich und eine im Integral enthaltene Fensterfunktion ![]() , die innerhalb der Bandbreite Eins und außerhalb Null ist.
, die innerhalb der Bandbreite Eins und außerhalb Null ist.
![]()
Diese Gleichung entspricht genau der Fouriercosinustransformation. Die inverse Fouriercosinustransformation entspricht bei geraden Funktionen der Fouriercosinustransformation und ist definiert durch
![]()
Für gerade Funktionen entspricht die Fouriercosinustransformation genau der komplexen Fouriertransformation, da die nach der EULERschen Formel enthaltenen Sinusanteile nur ungerade Funktionen oder ungerade Anteile einer Funktion repräsentieren, die bei rein geraden Funktioen verschwinden. Die letzte Gleichung läß sich daher auch schreiben als
![]()
Mit dieser Gleichung läßt sich aus dem Interferogramm I(x) das Spektrum ![]() berechnen.
berechnen.
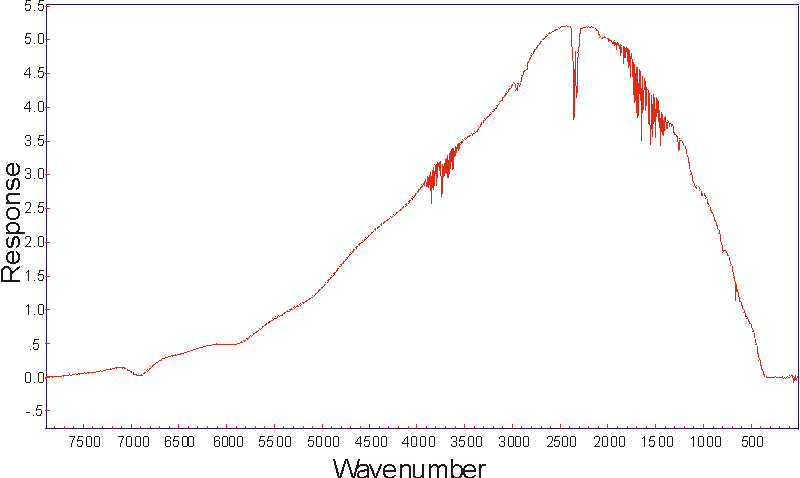
Dieses Spektrum entspricht allerdings noch nicht dem Transmissionsspektrum oder Extinktionsspektrum einer Probe. Vielmehr ist dies das Einstrahlspektrum, das die Energieverteilung der Lichtquelle, die Transmissionsfunktion des Spektrometers und die Empfindlichkeit des Detektors beinhaltet.
Das Extiktionsspektrum einer Probe berechnet sich durch Aufnahme des Einstrahlspektrums der Referenz (auch Background) und des Einstrahlspektrums der Probe. Dies sei nachfolgend am Beispiel des Extinktionsspektrums von HCl und DCl dargestellt. Die Referenzmessung erfolgte an Stickstoff
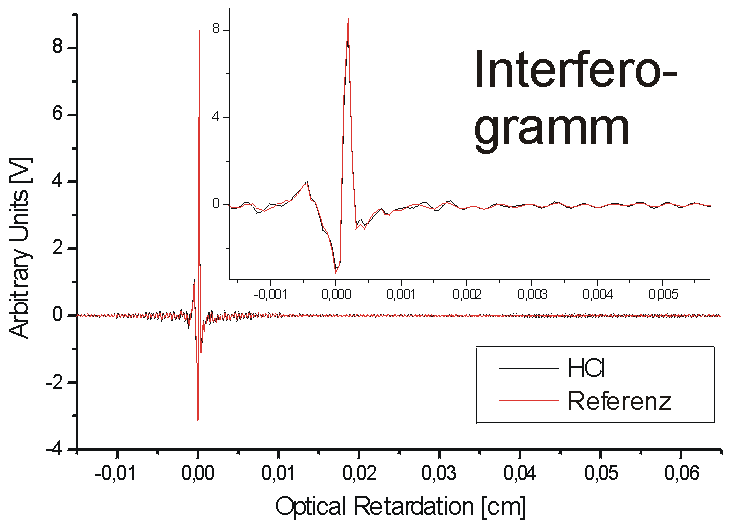
Obenstehendes Bild zeigt die Interferogramme der Probe und der Referenz. Da das Interferogramm idealerweise eine gerade Funktion ist, sind die Informationen beidseits des Nullpunktes der Spiegelverschiebung identisch. Es genügt daher, eine Seite des Interferogramms aufzunehmen.
Nach der Fouriertransformation ergeben sich die Einstrahlspektren zu
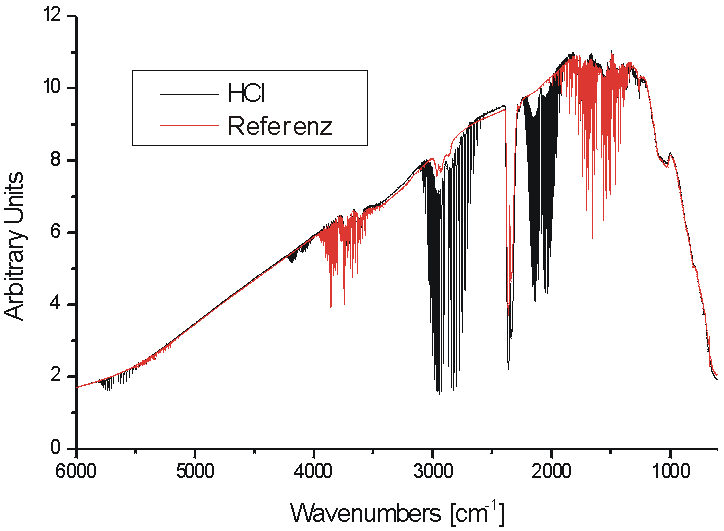
Berechnet man aus beiden Spektren das Extinktionsspektrum, ergibt sich
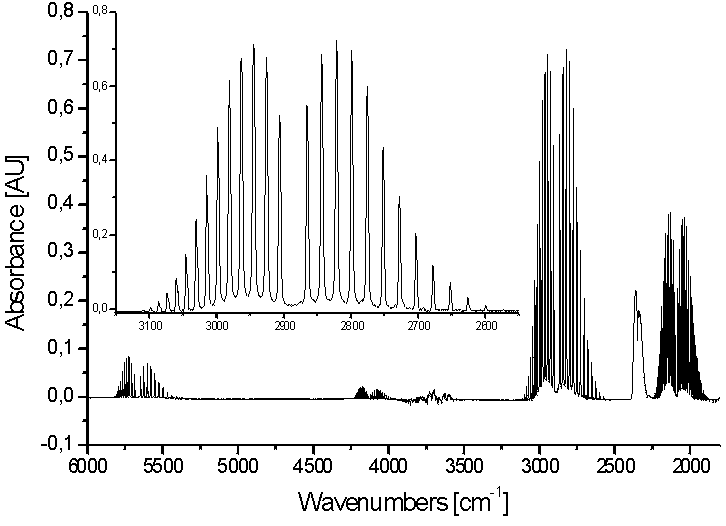
Zu sehen sind die Rotationsschwingungsspektren von HCl (2800 cm-1) und DCl (2200 cm-1) sowie deren erste Obertöne (HCl bei 5600 cm-1 und DCl bei 4400 cm-1) sowie Wasserbanden (3600 cm-1) und CO2-Banden (2300 cm-1).
| Griffith, de Haseth | Fourier Transfom Infrared Spectroscopy, John Wiley & Sons, New York, 1986 |
|
|
Fragen, Hinweise, Kritiken:
|